Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 131
Um gás de exaustão, a uma pressão total de 1 atm e a temperatura de 1400 K, contém CO2 e vapor de água a pressões parciais de 0,05 e 0,10 atm, respectivamente. Se o gás escoa através de uma longa chaminé com 1 m de diâmetro e 400 K de temperatura superficial, determine o fluxo térmico radiante líquido do gás para a superfície. Pode ser admitido um comportamento de corpo negro para a superfície da chaminé
Passo 1
É isso ai galerinhaaa !! Vamos continuando?
Bom, a questão nos pediu apenas o fluxo térmico radiante líquido entre o gás e a superfície da chaminé, ok?
Bom galerinha, a superfície está absorvendo irradiação emitida pelo gás e emitindo energia que será absorvida pelo gás , certo?
Se nós fizermos um balanço de energia:
A irradiação pode ser reescrita como:
Então:
Mexendo mais um pouquinho nessa equação:
Lembrando que:
Como o que nós estamos procurando é o , vamos só isolá-lo:
Shoooow !!
Agora vamos ver o que já temos?
Então nós só precisamos achar e !!
Passo 2
Para achar a emissividade do gás vamos dar uma olhada nesta figura aqui:
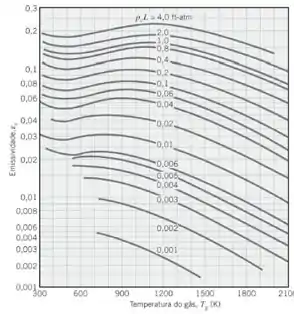
E para a água esta:
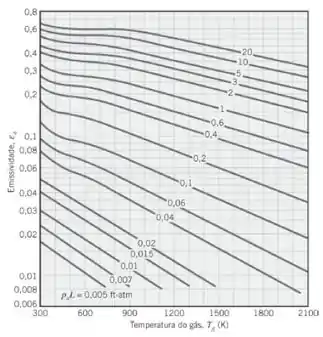
Para o cilindro:
Mas o gráfico nos pediu em transformando:
Interceptando no gráfico, quando
Mas o que nós queremos aqui é !!
E para isso nós vamos usar uma formulinha:
Para achar nós vamos precisar de mais um gráfico:
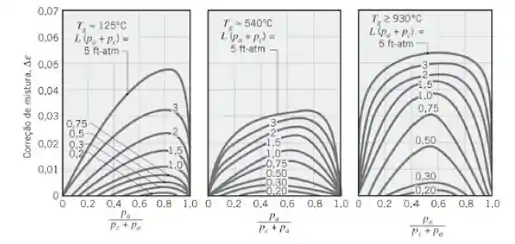
Calculando o que ainda não temos:
No último gráfico:
Ufaaaa !! Agora sim:
Passo 3
Para a absortividade nós temos uma fórmula para o vapor de água e para o gás!
Começando pelo vapor:
O coeficiente é obtido para o vapor com na figura abaixo:
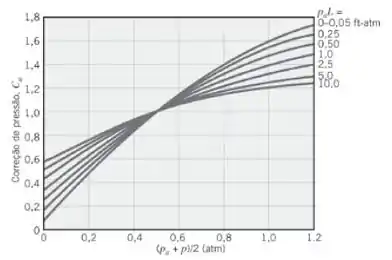
Se:
Então:
Substituindo:
No gráfico apresentado no Passo 2 para o vapor de água:
Passo 4
Para o gás:
O coeficiente é obtido para o vapor a uma pressão total de 1 atm e na figura abaixo:
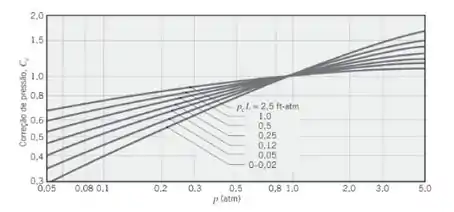
O que nos deu:
Vamos substituindo:
No gráfico apresentado no Passo 2 para o vapor de água:
Mas o que nós queremos aqui é !!
E para isso nós vamos usar uma formulinha:
Podemos calcular usando novamente a figura do Passo 2:
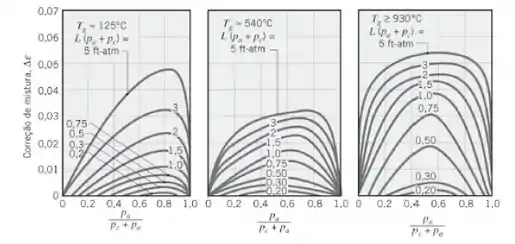
Usando os valores que já calculamos:
Como a temperatura é próxima de 125°C na superfície:
Então:
Eita lasqueira !!! Esta é grande ein !! Mas agora nós vamos substituir no calor e prontinhoo:
Shoooow !! Chegamos ao fim de mais umaa !!