Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 124
13-124 Água é descarregada a partir de um lago com 5 m de profundidade em um canal de concreto polido com uma inclinação do fundo de 0,004 através de uma comporta basculante
com uma abertura de 0,5 m de altura no fundo. Logo após o estabelecimento das condições de escoamento uniforme supercrítico, a água sofre um salto hidráulico. Determine a profundidade, a velocidade e o número de Froude do escoamento após o salto. Despreze a inclinação do fundo ao analisar o salto hidráulico.
Passo 1
Vamos pra mais uma questão e pra começar com o pé direito, vamos de esquiminha!!!
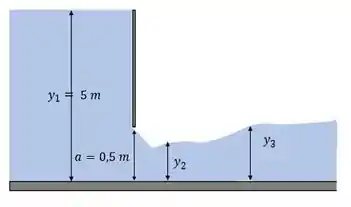
O problema pede pra a gente determinar a profundidade, a velocidade e o número de Froude do escoamento após o salto!
Para isso usamos as seguintes equações:
Mas tem alguns carinhas ai que a gente não conhece!! Vamos primeiro atás dessas variáveis!
Passo 2
Vamos começar calculando a vazão do escoamento, a gente vai precisar dela pra achar a profundidade do escoamento , para isso usamos:
O coeficiente de descarga pode ser determinado usando a figura 13-38 do livro, mas para isso precisamos calcular a seguinte relação:
Achamos então , o problema não nos da a largura do canal, então vamos assumir e lembrando que podemos substituir:
Neste caso a altura é igual ao raio hidráulico, , então podemos achar usando:
Para concreto polido , substituindo os dados:
Para resolver essa equação, vamos usar o solver o excel:
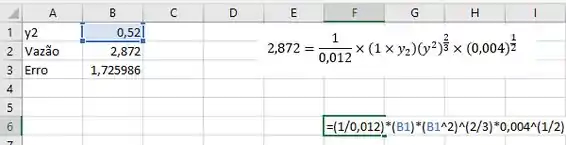
Com um chute de achamos !
Passo 3
Agora podemos calcular :
E :
E finalmente podemos calcular :
Substituindo, achamos:
Achamos a primeira!!!
Passo 4
Agora podemos achar a velocidade , com a equação da continuidade:
E pra acabar, o número de Froude:
Uhuuuuul!!!!