Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 13.Problemas - Ex. 123

13-123 Repita o Problema 13-122 para uma velocidade de 2 m/s após o salto hidráulico.

Passo 1

Opaa, o que temos aqui!!

Bora relembrar a questão anterior?!

Tinhamos água escoando através de uma comporta basculante e acontece um salto hidráulico, os dados então no nosso esqueminha:

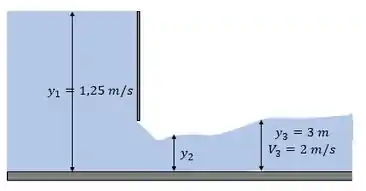
Queremos V ˙ , y 1 , y 2 e a taxa de dissipação de energia!

Vamos começar pela vazão:

V ˙ = V 3 A c 3 = V 3 b y 3

Como queremos a vazão por metro de largura, então vamos considerar b = 1   m :

V ˙ = 2 × 1 × 3 = 6   m 3 / s

Um já foi!!

Passo 2

Para achamos y 1 , a podemos usar a equação da continuidade:

y 1 = V 3 V 1 y 3 = 2 1,25 × 3 = 4,8   m

Para achamos y 2 usamos:

y 2 = 0,5   y 3 - 1 1 + 8 × F r 3 2

Mas não conhecemos F r 3 :

F r 3 = V 3 g y 3 = 2 9,81 × 3 = 0,3687  

Substituindo:

y 2 = 0,5 × 3 - 1 1 + 8 × 0 , 3687 2 = 0,667   m

Passo 3

A taxa de dissipação, que é dada por:

h L E s 2 = h L y 2 1 + F r 2 2 2

Mas para isso precisamos conhecer h L e F r 2 :

h L = y 2 - y 3 + V 2 2 - V 3 2 2 g

Substituindo:

h L = 0,667 - 3 + 8,994 2 - 2 2 2 × 9,81 = 1,586   m

Agora F r 2 :

F r 2 = V 2 g y 2 = 8,994 9,81 × 0,667 = 3,516

Agora sim:

h L E s 2 = 1,586 0,667 1 + 3,516 2 2

Calculando, achamos:

h L E s 2 = 0,331  

Resposta

V ˙ = 6   m 3 / s

y 1 = 4,8   m

y 2 = 0,667   m

h L E s 2 = 0,331    

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma pedrinha é abandonada em uma corrente de água que escoa em um canal retangular de 1,5 m de profundidade. Em um segundo, uma ondulação causada pela pedra é levada 3,9 m a jusante. Qual é a velocida
Ondas de superfície são causadas pela forma do objeto que toca apenas na superfície de uma corrente de escoamento de água, formando o padrão de onda mostrado. A profundidade da corrente é 150 mm. Dete
Verifique a equação dada na Tabela 11.1 para o raio hidráulico de um canal trapezoidal. Trace o gráfico da taxa R / y para b = 2m com inclinações do lado de 30° e 60° para 0,5my3m .
Ondas capilares (ondulações) têm pequena amplitude e comprimento de ondas, e são comumente vistas, por exemplo, quando um inseto ou uma pequena partícula atinge a superfície da água. Elas são ondas ge
O número de Froude caracteriza escoamento com uma superfície livre. Trace um gráfico, em escala logarítmica, da velocidade versus a profundidade para 0,1m / sV3m / s e 0,001my1m ; Trace a linha de F r