Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 92
Uma grossa parede feita em madeira de carvalho, inicialmente a 25 °C, é subitamente exposta a produtos de combustão para os quais = 800 °C e h = 20 W/(m² · K).
(a) Determine o tempo de exposição necessário para a superfície da parede atingir a temperatura de ignição de 400 °C.
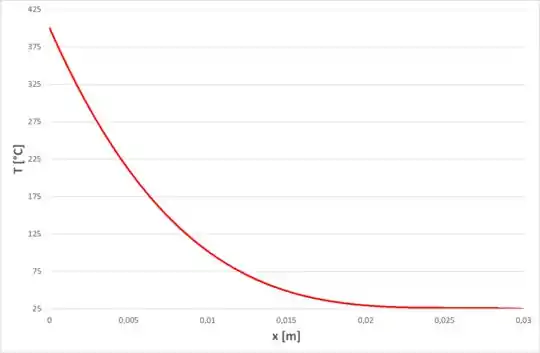
(b) Represente graficamente a distribuição de temperaturas T(x) na parede em t = 325 s. A distribuição deve se estender até a posição na qual T ≈ 25 °C.
Passo 1
Beleza! Nesse exercício, vamos modelar o problema como sendo um sólido semi-infinito com convecção na superfície. Sabendo disso, podemos usar a figura 5.8 apresentada nessa seção, que é dada a seguir:
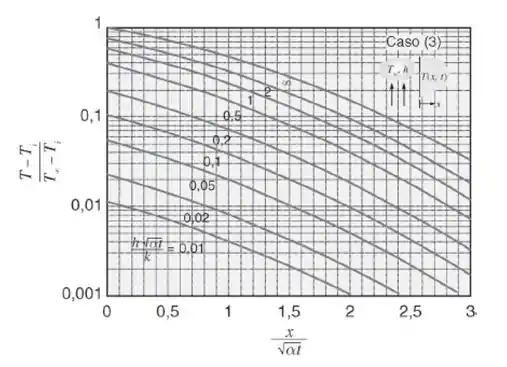
Então, como estamos interessados na temperatura na superfície, temos:
Então, iremos analisar a extremidade esquerda do gráfico. Agora, precisamos determinar a relação adimensional de temperaturas, que será dada por:
Substituindo os valores conhecidos, lembrando que estamos interessados no tempo quando a superfície da parede atingir a temperatura de 400 °C, então temos:
Passo 2
Então, olhando o gráfico, podemos estimar uma linha para a relação , e no nosso caso, olhando o gráfico, podemos ver que nosso ponto fica entre as curvas de valor 0,5 e 1, e aproximadamente no meio delas, então, nesse caso, vamos adotar:
Então, isolando o tempo dessa equação, temos:
Agora, precisamos buscar os valores das propriedades da madeira de carvalo, a temperatura de 25 ° C ≈ 300 K, dessa forma, recorrendo à tabela A.3 do apêndice A, temos os seguintes valores:
E, com esses valores, podemos calcular a difusividade térmica , dada por:
Então, substituindo os valores conhecidos na equação para o tempo, chegamos em:
Passo 3
Agora, na letra (b), para representar a distribuição de temperatura na parede em t = 325 s, devemos utilizar a equação 5.63 vista nesse capítulo, que é modelada para um sólido semi-infinito com convecção na superfície, e dada a seguir:
No nosso caso, estamos interessados em avaliar a temperatura até o ponto em que ela seja aproximadamente igual a 25 °C para um tempo fixo de 325 segundos. Dessa forma, com a equação acima, podemos modelar a distribuição de temperatura como:
