Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 97
Quando um metal fundido é derramado sobre um molde que é um péssimo condutor de calor, a resistência dominante à transferência de calor está na parede do molde. Considere condições nas quais um metal líquido está se solidificando em um molde com paredes espessas, com condutividade térmica e difusividade térmica . A massa específica e o calor latente de fusão do metal são designados por e , respectivamente, e tanto no seu estado fundido quanto no estado sólido a condutividade térmica do metal é muito maior do que a do molde.
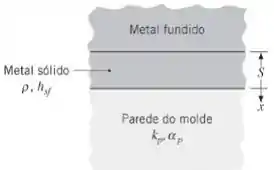
Imediatamente antes do início da solidificação a parede do molde se encontra a uma temperatura inicial uniforme e o metal fundido está em qualquer posição na sua temperatura de fusão (ponto de fusão). Após o início da solidificação, há transferência de calor por condução para dentro da parede do molde e a espessura do metal solidificado, , aumenta com o passar do tempo .
(a) Esboce a distribuição de temperaturas unidimensional, na parede do molde e no metal em e em dois instantes subsequentes durante o processo de solidificação. Indique claramente todas as hipóteses que forem feitas.
(b) Obtenha uma relação para a variação da espessura da camada sólida em função do tempo , expressando o seu resultado em termos dos parâmetros apropriados do sistema.
Passo 1
Ora ora, o que nós temos aqui? O enunciado nos fornece as propriedades da parede do molde e um metal solidificante. E precisamos encontrar a distribuição da temperatura na parede do molde em momentos selecionados, e a expressão para variação da espessura da camada sólida.
Passo 2
Para resolver essa questão, vamos assumir que:
(1) A parede do molde pode ser aproximada como um meio semi-infinito no qual existe condução dimensional;
(2) A camadas de metal sólido e líquido permanecem à temperatura de fusão durante a solidificação (resistência insignificante à transferência de calor por condução através do sólido);
(3) A resistência de contato é desprezível na interface molde / metal;
(4) As propriedades são constantes.
Na letra (a), queremos esboçar a distribuição de temperaturas unidimensional. Que é representado por:
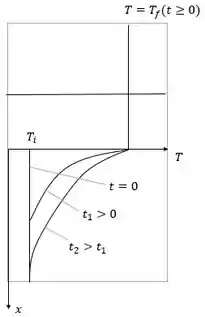
Como mostrado na imagem acima, a temperatura permanece praticamente uniforme no metal (em ) durante todo o processo, enquanto a temperatura e a inserção da temperatura aumentam com o tempo na parede do molde.
Passo 3
Na letra (b) queremos uma relação para a variação da espessura da camada sólida em função do tempo . Ao realizar um balanço de energia para uma superfície de controle sobre a camada sólida, a energia latente liberada devido à solidificação na interface sólido / líquido é equilibrada pela condução de calor no sólido,
Onde,
E,
Integrando em ,
E isolando S, temos:
Resposta
(a)
(b)