Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 104
A hélice de um barco de propulsão a ar, usado no parque nacional de Everglades, na Flórida, movimenta ar à taxa de 50 kg/s. Quando em repouso, a velocidade da corrente de ar atrás da hélice é de 45 m/s em um local onde a pressão é atmosférica. Calcule (a) o diâmetro da hélice, (b) o empuxo produzido em repouso e (c) o empuxo produzido quando o barco move para a frente a 15 m/s, se a vazão mássica através da hélice permanece constante.
Passo 1
Tá legal! Vamos começar o exercício ilustrando o problema, conforme vimos nessa seção do livro, então, temos:
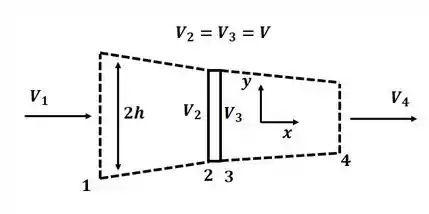
Então, a partir da equação do equilíbrio de momento na direção apresentado no capítulo 4, temos:
Então, para o sistema de controle desenhado, onde podemos desprezar as forças de campo na direção , ou seja, , e temos regime permanente, então podemos zerar a derivada parcial no tempo, temos:
No entanto, devido a continuidade do sistema, sabemos que a vazão mássica é constante, então, temos:
Então, substituindo isso na equação anterior, temos:
Então, considerando o caso onde o barco está em repouso, temos , e então:
Essa é a resposta da letra b)
Passo 2
Para resolver a letra a), vamos recorrer à relação vista no exemplo 10.13 dessa seção, então:
E, para o caso onde o barco está em repouso com , temos:
Então, da equação da continuidade escrita no passo 1, temos:
Substituindo os valores conhecidos, podemos encontrar o diâmetro da hélice:
Passo 3
Agora para resolver a letra c), precisamos retornar à equação da velocidade descrita no passo 2:
Substituindo os valores conhecidos, temos:
E, agora, usando a equação para o empuxo encontrada no passo 1, temos:
Passo 4
Agora, para analisar se a vazão mássica através da hélice permanece constante, basta olhar para a equação da vazão mássica usada no passo 2:
Nesse caso, a vazão mássica depende da densidade do fluido, que obviamente não mudou de um caso para o outro, do diâmetro da hélice, que também não mudou e da velocidade no ponto V, que conforme vimos, permanece constante. E isso faz sentido, devido à continuidade do sistema.