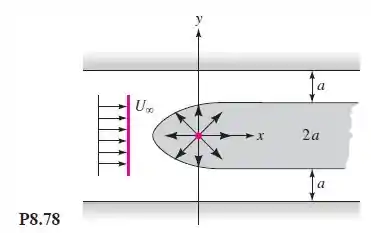
Indique o sistema de imagens necessário para construir o escoamento de uma corrente uniforme em torno de um semicorpo de Rankine confinado entre duas paredes paralelas, como na Figura . Para as dimensões particulares dessa figura, avalie a posição do nariz do semicorpo resultante.

E aí, tudo bem? Bora matar essa questão!

Esse é um problema mais conceitual, pensar assim, se as duas paredes “contem a emissão” a força necessária para causar esse efeito seriam infinitas fontes de força segmentadas pela mesma distancia sofrendo o mesmo escoamento, assim temos:

Como a força de emissão cabe dentro de uma coluna de tamanho temos:

Lembrando que a distancia até o nariz denota o ponto de estagnação, assim temos uma série basiquinha! hehe

Resolvendo a série, obtemos o seguinte resultado:

Por isso precisamos de uma visão mais abrangente

Isso é tudo pessoal, conseguimos mais uma! \o/