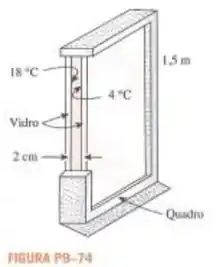
Uma janela vertical de painel duplo de de altura e de largura é composta de duas folhas de vidro separadas por um espaço de ar de a pressão atmosférica. Se as temperaturas da superfície do vidro através da abertura de ar são medidas como e determine a taxa de transferência de calor através da janela por (a) convecção natural e (b) radiação. Além disso, determine o valor de isolamento dessa janela de tal forma que, multiplicando-se o inverso do valor pela área da superfície e a diferença de temperatura, obtenha-se a taxa total de transferência de calor pela janela. A emissividade efetiva para uso em cálculos de radiação entre duas grandes placas de vidro paralelas pode ser de .

Primeiro, vamos começar calculando a temperatura média do ar entre os painéis. Assim temos:

Aqui,  é a temperatura média do ar,  é a temperatura da superfície interna do vidro e  é a temperatura da superfície interna do outro vidro. Substituindo os dados, temos:

Com a temperatura média, podemos obter as propriedades do ar na temperatura média da  usando a tabela A-15 “Propriedades do ar à pressão de 1 atm” do livro didático usando o método de interpolação.

Condutividade térmica:

Viscosidade cinemática:

Número Prandtl:

a) Vamos também calcular o coeficiente de expansão do volume usando a seguinte expressão:

Onde é a temperatura de filme que neste caso é mesma que a temperatura média. precisa estar em kelvin.

Agora, vamos calcular o número de Rayleigh usando a seguinte relação:

Aqui,  é o número de Rayleigh,  é a aceleração devido à gravidade, é a Viscosidade cinemática e é o comprimento característico. Substituindo os termos da equação pelos dados calculados anteriormente, temos:

Vamos também calcular o número de Nusselt usando a seguinte relação:

Aqui, é o número de Nusselt,  é a altura da janela e  é o espessura do espaço de ar na janela. Substituindo os termos da equação pelos dados coletados, temos:

Agora, podemos calcular o coeficiente de transferência de calor usando a seguinte relação:

Aqui,  é o coeficiente de transferência de calor, é a condutividade térmica. Substituindo os termos pelos dados encontrados, temos:

Com o coeficiente de transferência de calor encontrado, podemos calcular a taxa de transferência de calor por convecção. Assim temos:

Aqui,  é a taxa de transferência de calor por convecção e é a área da superfície. Substituindo os termos da equação acima pelos dados obtidos, temos:

Portanto, a taxa de transferência de calor por convecção é .

b) Agora, vamos calcular a taxa de transferência de calor por radiação usando a seguinte relação:

Aqui,  é a taxa de transferência de calor por radiação,  a emissividade efetiva e  é a constante de Boltzmann. Substituindo os termos da equação acima pelos dados obtidos, temos:

Portanto, a taxa de transferência de calor por radiação é .

Assim, podemos calcular a taxa total de transferência de calor da seguinte maneira:

Aqui,  é a taxa total de transferência de calor. Assim temos:

Agora, podemos calcular a resistência à transferência de calor comparando a transferência de calor total à transferência de calor condutora.

Substituindo os termos da equação pelos dados encontrados, temos:

Portanto, o valor  do isolamento da janela é .