Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 55
O lado em contato com a água da parede de uma represa com 100 m de comprimento é um quarto de círculo com raio de 10 m. Determine a força hidrostática sobre a barragem e sua linha de ação quando ela estiver cheia até a borda.
Passo 1
Oi pessoal, tudo bem?
Bem, inicialmente assumimos que:
- A pressão atmosférica atua nos dois lados da barragem e, portanto, pode ser ignorada nos cálculos.
Consideramos que a densidade da água é: .
E do problema, temos:
Consideramos o diagrama de corpo livre do bloco líquido encerrado pela superfície circular da barragem e suas projeções verticais e horizontais. As forças hidrostáticas que atuam nas superfícies dos planos vertical e horizontal, bem como peso do bloco líquido são:
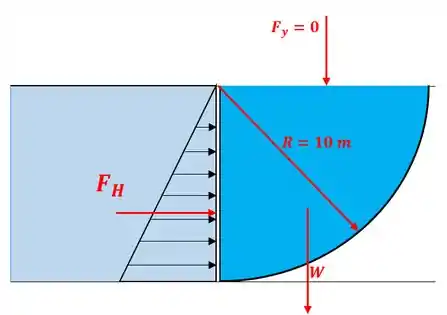
Passo 2
Então, a força horizontal na superfície vertical:
Assim, substituindo os valores e resolvendo, temos:
A força vertical na superfície horizontal é zero, uma vez que coincide com a livre
superfície da água. O peso do bloco de fluido por m de comprimento é (W):
Substituindo os termos e resolvendo, temos:
Passo 3
Então, a magnitude e a direção da força hidrostática que atua na superfície da barragem tornam-se:
E
Portanto, a linha de ação da força hidrostática passa pelo centro da curvatura da barragem, perfazendo 57,5 ° para baixo a partir da horizontal.
Resposta
Portanto: e a linha de ação da força hidrostática passa pelo centro da curvatura da barragem, perfazendo 57,5 ° para baixo a partir da horizontal.