Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 54

Uma sala no nível inferior de um navio de cruzeiro tem uma janela circular com 30 cm de diâmetro. Se o ponto médio da janela estiver 5 m abaixo da superfície da água, determine a força hidrostática que age sobre a janela e o centro de pressão. Tome a densidade da água do mar como 1,025.

Passo 1

Oi pessoal, tudo bem?

Bem, inicialmente assumimos que:

  1. A pressão atmosférica atua nos dois lados da janela e, portanto, pode ser ignorada nos cálculos.

De acordo com o enunciado, a gravidade específica da água é 1,025, então consideramos que a densidade da água é: ρ H 2 O = 1025   k g / m ³ .

E do problema, temos:

h = 5   m         |     b = 4   m       |         A = h * b = 20   m 2   |

Podemos representar um esboço da força atuante na sala do navio:

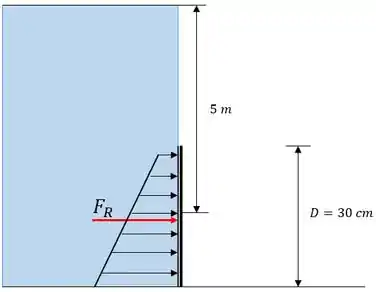
Passo 2

Letra a) A pressão média na superfície é a pressão no centróide (ponto médio) da superfície e é determinado como:

P c = ρ H 2 O * g * h

Substituindo os termos e resolvendo a equação:

P c = 1025 * 9,81 * 5 = 50,276   k N m 2

Assim, a força hidrostática resultante na janela é:

F R = P c A = P c * π D 2 4 = 50,276 * 10 3 * π 0,3 2 4           → F R = 3,55   k N

A linha de ação da força passa pelo centro de pressão, cuja vertical distância da superfície livre é determinada a partir de:

y p = y c + I x x y c A = y c + π R 4 / 4 y c π R ²  

Assim, substituindo os valores e resolvendo, temos:

y p = 5 + π * 0,15 4 / 4 5 * π * 0,15 ²                                     → y p = 5   m

Para pequenas superfícies profundas em um líquido, o centro de pressão quase coincide com o centróide da superfície. Aqui, de fato, com três dígitos significativos na resposta final, o centro de pressão e o centróide são coincidentes.

Resposta

Portanto:

F R = 3,55   k N

y p = 5   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é força de flutuação? O que a causa? Qual é a intensidade da força de flutuação que age sobre um corpo submerso cujo volume é V ? Quais são a direção e a linha de ação da força de flutuação?
Considere duas bolas esféricas com 5 cm de diâmetro – uma feita de alumínio e a outra de ferro – submersas em água. As forças de flutuação que agem sobre essas duas bolas serão iguais ou diferentes? E
A densidade de um líquido deve ser determinada por um velho hidrômetro cilíndrico com 1 cm de diâmetro cujas marcas de divisão foram completamente apagadas. A princípio o hidrômetro é colocado na água
O volume e a densidade média de um corpo de forma irregular devem ser determinados usando-se uma balança de mola. O corpo pesa 7200 N no ar e 4790 N na água. Determine o volume e a densidade do corpo.
Considere um grande bloco de gelo cúbico flutuando na água do mar. As densidades do gelo e da água do mar são 0,92 e 1,025, respectivamente. Se uma parte com 10 cm de altura do bloco de gelo ficar aci