Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 180
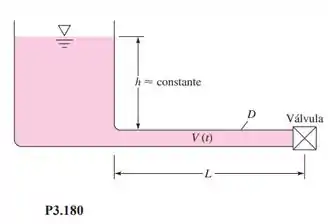
O líquido incompressível no grande tanque da Figura P3.180 está em repouso quando, em , a válvula é aberta para a atmosfera. Admitindo (velocidades e acelerações desprezíveis dentro do tanque), use a equação de Bernoulli para escoamento não permanente e sem atrito para deduzir e resolver uma equação diferencial para V(t) no tubo.
Passo 1
Vamos começar aplicando Bernoulli em um ponto na superfície do tanque (ponto 1) e em um ponto na saída do tanque (ponto 2), este é um problema em regime transiente:
Os dois pontos possuem pressão igual a atmosférica, vamos utilizar o referencial no ponto 2 e é aproximadamente zero pelo diâmetro do tanque.
O termo pode ser aproximado para , então:
A solução desta integral de primeira ordem com e é:
Resposta
Exercícios de Livros Relacionados
Um tanque pressurizado de água com 2 m de diâmetro tem um orifício com 10 cm de diâmetro na parte inferior, onde a água é descarregada para a atmosfera. Inicialmente o nível da água está 3 m acima da
Ar a 100 kPa e 25°C escoa em um duto horizontal de seção transversal variável. A coluna d’água do manómetro que mede a diferença entre duas seções tem um deslocamento vertical de 8 cm. Se a velocidade
Sua empresa está montando uma experiência que envolve a medição da vazão do ar em um duto, e você precisa fornecer a instrumentação necessária. Pesquise as técnicas e dispositivos disponíveis para a m
Projetos auxiliados por computador, o uso de materiais melhores e as técnicas de manufatura aperfeiçoadas resultaram em um aumento incrível da eficiência de bombas, turbinas e motores elétricos. Entre
Reconsidere o Problema 5-89. Usando o EES (ou m outro aplicativo), investigue o efeito da altura do tanque sobre a velocidade da descarga inicial da água do tanque completamente cheio. Deixe a altura