Ar a 100 kPa e 25°C escoa em um duto horizontal de seção transversal variável. A coluna d’água do manómetro que mede a diferença entre duas seções tem um deslocamento vertical de 8 cm. Se a velocidade da primeira seção é baixa e o atrito é desprezível, determine a velocidade na segunda seção. Da mesma forma, se a leitura do manómetro tem um erro possível de ± 2 mm, faça uma análise de erro para estimar o intervalo de validade da velocidade encontrada.

Pronto, agora vamos analisar o problema, ok? Podemos primeiramente imaginar o duto do problema sendo do mesmo formato que do problema 5-83, da forma:

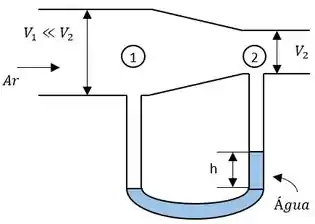
Assim, tomamos os pontos 1 e 2 ao longo da linha central do tubo sobre os dois tubos do manômetro. Observando que (ou, os efeitos de elevação são desprezíveis para gases), e , a equação de Bernoulli entre os pontos 1 e 2 fornece:

Deixamos que a altura diferencial do manômetro de água seja h. Então a diferença de pressão também pode ser expressa como:

Assim, combinando as equações 1 e 2, temos:

Porém, ainda não sabemos o para encontrar a velocidade na segunda seção.

Podemos, portanto, utilizar a equação geral dos gases para encontrar a densidade específica do ar, assim:

Assim, substituindo os valores na equação 3, temos:

Portanto, a velocidade do ar aumenta de um nível baixo na primeira seção para 36,6 m/s na segunda seção.

Agora, observando a análise de erro: Devemos entender como a altura(leitura) do manómetro se relaciona com a velocidade encontrada.

Se observarmos a Eq. (3), podemos ver que a velocidade é proporcional à raiz quadrada da altura diferencial do fluido do manômetro. Ou seja, .

Onde:

Assim, tomando o diferencial:

Dividindo-se tudo por , temos:

Por fim, a razão nos informa o erro para estimar o intervalo de validade da velocidade encontrada. Então:

Portanto, a incerteza na velocidade correspondente a uma incerteza de 2 mm na altura diferencial da água é 1,3%, o que corresponde a:

Então a velocidade de descarga pode ser expressa como: