Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 3.Problemas - Ex. 157

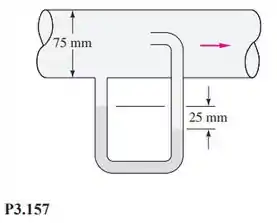
O fluido manométrico da Figura P3.157 é o mercúrio. Calcule a vazão volumétrica no tubo se o fluido que escoa é (a) gasolina e (b) nitrogênio a 20°C e 1 atm.

Passo 1

Antes de tudo, pra ficar mais fácil, vamos especificar alguns pontos no sistema:

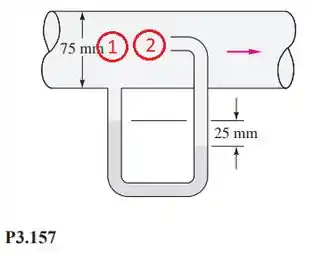
O ponto 1 lê a pressão estática do sistema e o ponto 2, que é o tubo de Pitot, lê a pressão de estagnação.

Agora que especificamos estes pontos podemos fazer a consideração que no ponto 2 a velocidade do fluido será zero ( V 2 = 0 ), porque é um ponto de estagnação.

Mais uma coisinha antes de ir pro próximo passo, o problema disse que tanto a gasolina quanto o nitrogênio estão a 20°C e a 1 atm, logo, a gente pode conseguir as suas densidades. Para a gasolina basta uma pesquisa, mas lembre de utilizar as condições de temperatura e pressão especificadas. Pesquisando aqui achei que ρ g a s o l i n a = 715 k g m 3 .

Para o nitrogênio vai ser um pouco mais complicado porque nestas condições ele é um gás, então precisaremos recorrer a equação dos gases ideais, onde:

ρ = p M M R T

Como o exercício já nos deu a pressão e a temperatura (lembrando de converter a pressão para Pascal p = 101325   P a e a temperatura para Kelvin T = 293   K ) só vamos precisar da constante dos gases e a massa molar do nitrogênio. A massa molar do nitrogênio é M M n i t r o g ê n i o = 28,00 k g k m o l e a constantes do gases é R = 8,314 k J k m o l * K = 8314 J k m o l * K . Agora é só substituir:

ρ n i t r o g ê n i o = p M M n i t r o g ê n i o R T = 101325 * 28,00 8314 * 293

ρ n i t r o g ê n i o = 1,165 k g m 3

Passo 2

A vazão volumétrica é escrita da seguinte maneira:

Q = V * A

Onde V é a velocidade e A é a área da seção transversal. Como o exercício pede a vazão volumétrica no tubo, vamos precisar encontrar V no ponto 1. A área da seção transversal nesse ponto pode ser escrita (lembrando que o diâmetro nesta região é D = 75   m m = 0,075   m ):

A 1 = π R 1 2 = π D 1 2 4 = π 0,075 2 4 = 0,00442   m 2

Passo 3

Agora, pra gente conseguir prosseguir vamos precisar achar V 1 , mas pra isso é só aplicar Bernoulli entre dois pontos e obviamente vamos fazer isso entre os pontos 1 e 2, e melhor ainda, vamos aplicar em uma região onde z 1 = z 2 , ou seja, os termos com a altura na equação de Bernoulli se anularam ( ∆ z = 0 ). Lembrando também que V 2 = 0 :

p 1 + ρ 2 V 1 2 + ρ g z 1 = p 2 + ρ 2 V 2 2 + ρ g z 2

p 1 + ρ 2 V 1 2 = p 2

Onde ρ é a densidade da gasolina ou do nitrogênio.

Isolando V 1 :

V 1 = 2 * p 2 - p 1 ρ

E agora, quais seriam as pressões? Bom, isto é simples, basta saber que as pressões no ponto 1 e 2 vão ser as mesmas que as pressões nos pontos A e B abaixo:

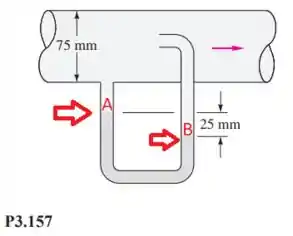
Com isso em mente é só calcular a pressão hidrostática entre os pontos A e B que vamos encontrar direto o termo p 2 - p 1 .

p B - p A = ( ρ m e r c ú r i o - ρ ) g h

A densidade do mercúrio é ρ m e r c ú r i o = 13600 k g m 3 , a altura em metros h = 0,025   m , a aceleração da gravidade g = 9,81 m s 2 e p B - p A = p 2 - p 1

p 2 - p 1 = 13600 - ρ * 9,81 * 0,025

Substituindo essa igualdade no valor de V 1 :

V 1 = 2 * p 2 - p 1 ρ = 2 * 13600 - ρ * 9,81 * 0,025 ρ = 0,4905 * 13600 - ρ ρ

Passo 4

Pessoal, a partir daqui nós vamos ter dois casos, um pra gasolina e outro para o nitrogênio, e a única coisa que vai mudar será a densidade.

Começando com a gasolina:

V 1 = 0,4905 * 13600 - ρ g a s o l i n a ρ g a s o l i n a = 0,4905 * 13600 - 715 715 = 2,97 m s

Para o nitrogênio vai ficar:

V 1 = 0,4905 * 13600 - ρ n i t r o g ê n i o ρ n i t r o g ê n i o = 0,4905 * 13600 - 1,165 1,165 = 75,67 m s

Passo 5

Agora é só achar as vazões volumétricas. Começando com a gasolina:

Q g a s o l i n a = V 1 * A 1 = 2,97 * 0,00442 = 0,013 m 3 s

E para o nitrogênio a vazão é:

Q n i t r o g ê n i o = V 1 * A 1 = 75,67 * 0,00442 = 0,334 m 3 s

Resposta

Para a gasolina V 1 Q g a s o l i n a = 0,013 m 3 s , para o nitrogênio Q n i t r o g ê n i o = 0,334 m 3 s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A pressão manométrica da água nos reservatórios de uma cidade em determinado local é de 400k P a . Determine se esse reservatório pode fornecer água para vizinhança que esta 50m acima desse local.
Uma bomba manual de bicicleta pode ser usada como um atomizador para gerar uma nevoa fina de tinta ou pesticida forçando o ar a uma alta velocidade através de um pequeno orifício e colocando um tubo c
Usando um canudinho flexível e uma régua, explique como você mediria a velocidade de escoamento da água de um rio.
A potência gerada por uma turbina de vento é proporcional ao cubo da velocidade do vento. Inspirado pela aceleração de um fluido em um bocal, alguém propõe a instalação de um gabinete redutor para cap
O que é carga de bomba útil? Como ela se relaciona à entrada de potência na bomba?