Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 61
Uma longa barra de conexão (haste cilíndrica usada para fazer conexões elétricas) de diâmetro D é instalada no interior de um grande conduíte, que tem uma temperatura superficial de 30°C e no qual o ar ambiente tem temperatura T∞ = 30°C. A resistividade elétrica, ρe (μΩ · m), do material da barra é uma função da temperatura, na forma ρe = ρe,o [1 + α(T − To)], onde ρe,o = 0,0171 μΩ · m, To = 25°C e α = 0,00396 K−1. Há convecção natural entre a barra e o ar ambiente, e o coeficiente de transferência de calor depende do diâmetro da barra, assim como da diferença de temperaturas entre a sua superfície e o ambiente. A relação que governa esta dependência tem a forma h = C D–0,25 (T – T∞)0,25, sendo C = 1,21 W · m–1,75 K–1,25. A emissividade da superfície da barra é ∞ = 0,85.
(a) Reconhecendo que a resistência elétrica por unidade de comprimento da barra é R’e= ρe/Asr, em que Asr é a área da sua seção transversal, calcule a capacidade de transporte de corrente de uma barra com 20 mm de diâmetro, se a sua temperatura não puder exceder a 65°C. Compare a importância relativa das transferências de calor por convecção natural e por radiação.
(b) Para avaliar o compromisso entre a capacidade de transporte de corrente, a temperatura operacional e o diâmetro da barra, para diâmetros de 10, 20 e 40 mm, faça um gráfico da temperatura da barra T como uma função da corrente no intervalo 100 ≤ I ≤ 5000 A. Também coloque no gráfico a razão entre a transferência de calor por convecção e a transferência de calor total.
Passo 1
Vamo analisar o enunciado junto pra entender o que ele quer de você.
Temos uma haste cilíndrica de diâmetro , por onde passa uma corrente elétrica, está insierida em um conduíte de temperatura e submetido à convecção com o ar a , conforme demonstra o esquema ilustrativo abaixo:
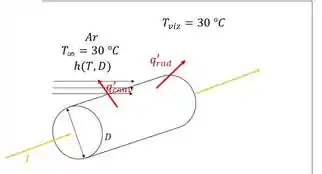
Esse problema quer que a gente calcule o valor da corrente que passa na haste para uma temperatura de na sua superfície, além de calcular a razão entre as transferências de calor por convecção natural e por radiação e, por fim, traçar gráficos da temperatura da parede pela corrente e da porcentagem de transferência de calor por convecção pela temperatura da parede.
Pra isso, a partir desse esquema ilustrativo acima, podemos fazer um balanço de energia integral por unidade de comprimento:
Sendo:
- , que é a fórmula pra potência elétrica que a gente vê no ensino médio ou em matérias de Eletrotécnica;
- , que é uma soma das taxas por unidade de comprimento das formas de transferência de calor condutiva e radiante que ocorrem na haste.
Vamos lembrar como calcula as taxas pra essas duas formas de transferência de calor e a resistência elétrica?
Para a taxa de calor convectiva, devemos utilizar a seguinte equação:
Onde o coeficiente de convecção é calculado como
Sendo .
Para a taxa de calor por radiação, devemos utilizar a seguinte equação:
Sendo a emissividade da haste, a constante de Stefan-Boltzmann. Lembrando que para calcular taxas de transferência de calor por radiação a gente tem que usar a temperatura em !
Por fim, a resistência elétrica pode ser calculada como:
Sendo a resistividade elétrica da haste , com , e .
Caramba, foi muita informação! Mas agora nos próximos passos a gente vai resolver as letras (a) e (b) do problema!
Passo 2
Primeiro, vamo resolver a primeira parte do item (a) do problema, considerando a haste de diâmetro e a temperatura da superfície igual a .
Vamos calcular as duas taxas de transferência de calor e a resistência térmica que eu te mostrei no passo anterior:
Substituindo no balanço, temos:
Substituindo os valores:
Passo 3
Agora, vamos resolver a segunda parte da letra (a).
A gente quer agora calcular a contribuição convectiva no total do calor perdido pela haste, a partir da seguinte equação:
Pronto, agora basta que a gente substitua os valores de e que a gente calculou no Passo 2:
Passo 4
Pra finalizar a questão, vamo resolver a letra (b) agora.
A gente tem que traçar gráficos da corrente pela temperatura da superfície e da porcentagem de transferência de calor por convecção pela superfície da parede para diâmetros de 10, 20 e 40 , montando funções pra isso.
Vamos fazer isso agora?
- Corrente em função da temperatura
- Porcentagem da taxa de convecção em função da temperatura
Indo no balanço do Passo 1, a gente pode chegar à seguinte expressão:
Agora, podemos traçar um gráfico no Excel variando a temperatura:
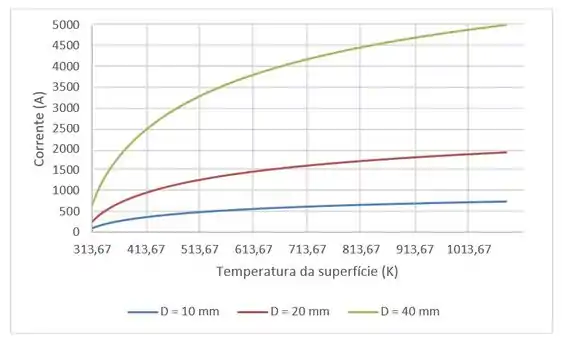
É possível ver que com o aumento do diâmetro da haste, maior a corrente que passa por ela para uma mesma temperatura da superfície. Ou seja, para que se atinja uma certa temperatura da superfície, quanto maior o diâmetro, mais corrente deveria passar pela haste.
Pela equação que a gente definiu no Passo 3, a gente pode chegar à seguinte expressão:
Agora, podemos traçar um gráfico no Excel variando a temperatura:
É possível ver que com o aumento do diâmetro da haste, menos a taxa convectiva será importante para a transferência de calor que está ocorrendo.
Ufa, finalmente matamos a questão juntos e acabamos!
Resposta
(a) A capacidade de transporte de corrente de uma barra com 20 é e a taxa de transferências de calor por convecção corresponde a do total.
(b) Os gráficos de Corrente pela Temperatura da superfície e da Porcentagem de transferência de calor por convecção pela Temperatura superfície são, respectivamente:
