Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 8.Problemas - Ex. 56
Uma forma de resfriar chips nas placas de circuito de um computador é colocar as placas em quadros de metal que permitem a passagem eficiente da condução térmica para placas frias, que suportam o arranjo. O calor gerado pelos chips é, então, dissipado pela transferência para a água que escoa através de passagens perfuradas nas placas frias. Como as placas são feitas com um metal de alta condutividade térmica (tipicamente alumínio ou cobre), pode-se considerar que elas estão a uma temperatura Ts,pf.
(a) Considere placas de circuitos fixadas a quadros frios de altura H = 750 mm e largura L = 600 mm, cada uma com N = 10 furos de diâmetro D = 10 mm. Se as condições operacionais mantêm a temperatura das placas Ts,pf = 32°C com uma vazão de água de m1 = 0,2 kg/s por furo com uma temperatura de entrada de Tm,ent = 7°C, quanto calor pode ser dissipado pelas placas de circuito?
(b) Para melhorar o resfriamento e assim permitir uma maior geração de potência sem um aumento correspondente das temperaturas do sistema, um esquema de resfriamento híbrido pode ser usado. O esquema prevê um escoamento forçado de ar sobre as placas de circuito no conjunto, bem como o escoamento de água através das placas frias. Considere condições nas quais Npc = 10 placas de circuito de largura W = 350 mm estão fixadas às placas frias e sua temperatura superficial média é de Ts,pc = 47°C, quando Ts,pf = 32°C. Estando o ar em escoamento paralelo sobre os circuitos com u∞ = 10 m/s e T∞ = 7°C, qual quantidade do calor gerado pelas placas de circuito é transferida para o ar?
Passo 1
Vamo analisar o enunciado junto pra entender o que ele quer de você.
Temos um placas de chip sendo resfriadas por placas frias com tubos em suas estruturas, por onde escoa água de forma a dissipar o calor gerado pelos chips.
Na letra (a), vamos calcular o quanto de calor pode ser dissipado pelas placas de circuito ao olharmos a transferência de calor na entrada e saída do tubo. Para isso, vamos olhar o esquema ilustrativo das placas frias com os valores de todas as variáveis que vamos utilizar ao longo do problema:
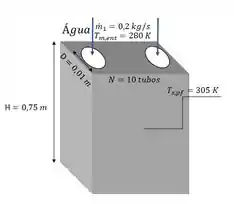
Para calcular esse calor dissipado, em primeiro lugar devemos calcular a temperatura de saída da água no tubo, depois de trocar calor, a partir da equação:
Depois, devemos calcular o calor transferido ao longo do tubo a partir da equação:
Como você notou, vamo precisar de algumas propriedades físicas da água pra resolver essas equações. A gente tem que buscar as propriedades da água líquida saturada na Tabela A.6 (página 640) a uma temperatura de aproximação de :
Na letra (b), vamos calcular o quanto de calor é transferido pelas placas de circuito ao ar. Para isso, vamos olhar o esquema ilustrativo das placas de chip com os valores de todas as variáveis que vamos utilizar ao longo do item (b):
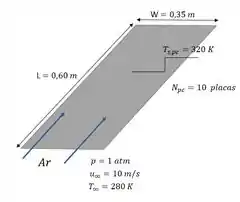
Pra calcular a taxa convectiva para cada placa, basta usar a equação abaixo:
Sendo a área superficial dos dois lados de uma placa, onde o ar escoa.
Pra resolver o item (b), vamo precisar buscar as propriedades do ar a 1 atm na Tabela A.4 (página 634) a uma temperatura média entre de :
Caramba, foi muito informação né? Agora a gente vai resolver a questão nos próximos passos.
Passo 2
Primeiro, vamo resolver o item (a).
Para calcular a temperatura média de saída da água (), precisamos calcular o coeficiente de transferência de calor a partir da equação:
Para saber qual correlação usar, devemos calcular primeiramente o número de Reynolds:
Esse valor do número de Reynolds indica um escoamento turbulento. Sendo assim, a correlação para calcular o número de Nusselt para um escoamento turbulento interno é:
Nosso problema satisfaz todas as restrições da equação. Sendo assim, o coeficiente de transferência de calor pode ser calculado como:
A seguir, vamos calcular a temperatura de saída da água do tubo:
Agora, vamos finalmente poder calcular a taxa de calor trocada em cada tubo:
Por fim, vamos calcular a taxa total de calor transferido somando os 20 tubos (10 tubos de cada lado, como mostra a imagem ilustrativa no enunciado da questão):
Passo 3
Agora, vamo resolver a letra (b).
Novamente, precisamos calcular o coeficiente de transferência de calor para as placas a partir da equação:
Para saber qual correlação usar, devemos calcular novamente o número de Reynolds:
Esse valor do número de Reynolds indica um escoamento laminar. Sendo assim, a correlação para calcular o número de Nusselt para um escoamento laminar em uma placa plana é:
Nosso problema satisfaz a restrição da equação. Sendo assim, o coeficiente de transferência de calor pode ser calculado como:
Agora, vamos finalmente poder calcular a taxa de calor trocada em cada placa:
Pra fechar a questão, vamos calcular a taxa total de calor transferido somando as 10 placas:
Pronto, matamos a questão junto ;)
Resposta
(a) A quantidade calor pode ser dissipado pelas placas de circuito é .
(b) A quantidade do calor gerado pelas placas de circuito que é transferida para o ar é .