Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 70

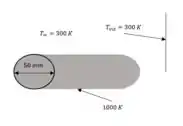
Longos bastões de aço inoxidável com 50   m m de diâmetro são préaquecidos até uma temperatura uniforme de 1000   K antes de serem pendurados em uma esteira aérea e transportados para uma operação de moldagem a quente. A esteira encontra-se em uma grande sala cujas paredes e o ar estão a 300   K .

( a ) Admitindo que o movimento linear do bastão tenha um efeito desprezível sobre a transferência de calor por convecção em sua superfície, determine o coeficiente convectivo médio no início do processo de transporte.

( b ) Se a emissividade da superfície do bastão é de ε   =   0,40 , qual é o coeficiente de transferência de calor por radiação efetivo no início do processo de transporte?

( c ) Considerando um coeficiente de transferência de calor constante e cumulativo (radiação mais convecção), correspondente aos resultados das partes ( a ) e ( b ) , qual é o tempo máximo permissível para o transporte se a temperatura no eixo central do bastão deve ser superior a 900   K para o processo de moldagem? As propriedades do aço são: k   =   25   W / ( m   ·   K ) e α   =   5,2   ×   10 - 6     m 2   / s .

( d ) As transferências de calor por convecção e radiação na realidade diminuem ao longo da operação de transporte. Levando em consideração essa redução, reconsidere as condições da parte ( c ) e obtenha uma estimativa mais precisa para o tempo máximo permissível para o transporte.

Passo 1

Muito bem galera, podemos ver que esse exercício é um pouco grande, mas muita calma, iremos por partes...

Vamos começar identificando os dados, sabemos do enunciado o material, as dimensões geométricas e a física presente.

Note que possuímos uma temperatura de 300 ° C presente na sala, porém em condições diferentes, pois temos o ar e as paredes, e no caso as paredes são nossas vizinhanças. Logo:

T v i z = 300 K ,   T ∞ = 300   K ,   D = 50   m m ,   ε b a s t ã o = 0,4

Do material:

k   =   25   W / ( m   ·   K ) e α   =   5,2   ×   10 - 6     m 2   / s

Para o ar precisaremos consultar a tabela A-4 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.), porém note que a temperatura uniforme é equivalente a temperatura de superfície.

Logo, calculando a temperatura de filme que estará presente pelo diferencial de temperatura:

T f = 1000 + 300 2 = 650   K

Agora sim, da tabela...

υ = 6,02 × 10 - 5 m 2 s ,   α = 8,73 × 10 - 5 m 2 s ,   k = 0,0497 W m ∙ K ,   P r = 0,69

Passo 2

Muito bem, agora para respondermos à questão ( a ) , na qual pede para determinarmos o coeficiente convectivo médio no início do processo de transporte, basicamente precisamos seguir uma receitinha:

  1. Identificar qual em situação nosso cilindro se encontra, logo será possível escolher qual equação usar para o número de Nusselt.
  2. Calcular o número de Nusselt.
  3. Estimar o coeficiente de convecção.

Bora lá?

Passo 3

Primeiramente, devemos nos atentar que a física do problema nada mais é uma troca de calor de forma natural, visto que não há nada influenciado no processo, somente as condições naturais do ambiente.

Porém, note que a troca de calor ocorrerá em um cilindro horizontal, como não conhecemos seu comprimento, mas por ser um bastão, iremos considerar como sendo um cilindro longo.

Logo, o número de Nusselt, será:

N u - D = 0,60 + 0,387 R a D 1 6 1 + 0,559 P r 9 16 8 27 2

Note que, precisamos determinar o Rayleigh (adimensional para convecção natural):

R a D = g β T s - T ∞ D 3 α υ = 9,8 m s 2 1 650 K 1000 - 300 K 0,05   m 3 6,02 × 8,73 × 10 - 10 m 4 s 2 = 2,51 × 10 5

O β presente na equação acima é conhecido como coeficiente de expansão térmica e é determinado pelo o inverso de T f .

Passo 4

Agora, determinado o número de Nusselt:

N u - D = 0,60 + 0,387 R a D 1 6 1 + 0,559 P r 9 16 8 27 2 = 0,60 + 0,387 2,51 × 10 5 1 6 1 + 0,559 0,69 9 16 8 27 2 = 9,9

Por fim...

N u - D = h - D k

h - = N u - D k D = 9,9 0,0497 W m ∙ K 0,05   m = 9,84 W m 2 ∙ K

Passo 5

Muito bem, agora vamos pra questão ( b ) , onde devemos calcular o coeficiente de transferência de calor por radiação.

Sabe aquela parede que citei no início? Por possuir uma emissividade ela terá uma influência na física do problema.

Bom, relembrando a equação para o cálculo do h r a d i a ç ã o :

h r a d i a ç ã o = ε σ ( T s + T v i z ) ( T s 2 + T v i z 2 )

h r a d i a ç ã o = 0,4 × 5,67 × 10 - 8 W m 2 ∙ K 4 1000 + 300 K 1000 2 + 300 2 k 2

h r a d i a ç ã o = 32,1 W m 2 ∙ K

Passo 6

Isso ai! Você está indo muito bem...

Na questão ( c ) , precisamos determinar o tempo máximo permissível de transporte do bastão e temos que considerar uma condição de projeto para o processo de moldagem, sendo ela:

A temperatura no eixo central do bastão deve ser superior a 900   K .

Logo, temos dois fatores para levar em conta o cálculo, os coeficientes de transferência de calor e o raio do bastão, visto que a condição de projeto se encontrar no eixo central, completando a física do problema.

Passo 7

Prosseguindo...Como devemos determinar um tempo, precisamos realizar uma análise transiente, por isso precisamos calcular algo que chamamos de Biot, e sua formulação está expressa abaixo:

B i = h L c k

L c = c o m p r i m e n t o   c a r a c t e r í s t i c o = r o 2   p o r   a d o t a r m o s   s e r   u m   c i l i n d r o   l o n g o

Logo...

B i = h - + h r a d i a ç ã o r o 2 k = 42 W m 2 ∙ K × 0,0125   m 25 W m ∙ K = 0,021  

Como o B i < 0,1 , iremos resolver a questão ( c ) pelo método do concentrado...

Obs: O método do concentrado só tem perturbação por convecção.

Passo 8

Método do concentrado:

T - T ∞ T s - T ∞ = e x p ⁡ ( - B i ∙ F o )

900 - 300   K 1000 - 300   K = 600   K 700   K = e x p ⁡ ( - 0,021 F o )

ln ⁡ 600   K 700   K = - 0,021 F o

F o = 7,34

Temos que:

F o = α t L c 2 = α t r o 2 2

F o = 7,34 = 8,73 × 10 - 5 m 2 s t 0,0125   m 2 = 0,0333 t

t = 221   s

Passo 9

Por fim...

A questão ( d ) só é possível resolve-la através de uma interação numérica, logo não iremos aborda-la.

Resposta

( a ) Coeficiente convectivo de transferência de calor:

h - = 9,84 W m 2 ∙ K

b Coeficiente convectivo de transferência de calor por radiação:

h r a d i a ç ã o = 32,1 W m 2 ∙ K

( c ) O tempo máximo permissível para o transporte se a temperatura no eixo central do bastão deve ser superior a 900 K para o processo de moldagem:

t = 221   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma lata de alumínio de bebida fria que está inicialmente a uma temperatura uniforme de 5°C. A lata tem 12,5 cm de altura e diâmetro de 6 cm. A emissividade da superfície externa da lata é 0
Em qual modalidade de transferência de calor o coeficiente de transferência de calor por convecção é mais elevado: convecção natural ou convecção forçada? Por quê?
Fisicamente, o que o número de Grashof representa? Em que o número de Grashof difere do número de Reynolds?
Considere um fluido cujo volume não se altera com a temperatura à pressão constante. O que você pode dizer sobre a transferência de calor por convecção natural nesse meio?
Considere dois fluidos, um com um grande coeficiente de expansão volumétrica e o outro com pequeno coeficiente. Em que fluido a superfície quente criará correntes de convecção naturais mais fortes? Po