Ar quente sai de um forno a uma velocidade de através de um duto de aço de parede delgada com de diâmetro. O duto atravessa o porão de uma casa e sua superfície externa, sem isolamento térmico, fica exposta ao ar quiescente e a uma vizinhança, ambos a .
Em uma posição do duto na qual a temperatura média do ar é de , determine a perda de calor por unidade de comprimento do duto e a temperatura na parede do duto. A emissividade da superfície externa do duto é de .
Se o duto for envolto por uma camada com de espessura de isolante térmico magnésia , que tem uma emissividade superficial de , quais serão a temperatura na parede do duto, a temperatura superficial externa e a perda de calor por unidade de comprimento do duto?
Passo 1
Iremos iniciar o exercício identificando os valores que o enunciado nos trás e a física do problema. Mas antes abaixo está um esboço para melhor visualização do problema:
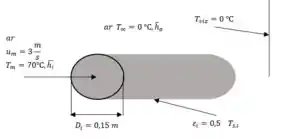
Primeira situação
Após aplicar o isolante térmico:
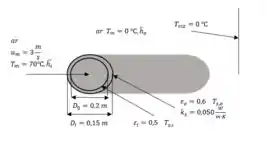
Segunda situação
Agora vamos lá, note que para esse exercício basta buscarmos os respectivos dados, para o fluido em que o duto se encontra, ou seja, para o ar. Porém temos dois ambientes, o interno e o externo.
Tabela A-4 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.).
, note que no exterior precisamos considerar um , ao contrário do caso anterior. Porém não temos a temperatura da superfície do duto...
Bom, nesses casos, você pode estimar uma temperatura para análise, porém pra se ter uma melhor aproximação, temos que o fluxo de calor será do interior do tubo para o ambiente, e a temperatura interior não é muito alta...
Logo, iremos considerar uma média de praticamente temperatura ambiente, logo:
Passo 2
Ainda identificando a física do problema, nesse exercício teremos então dois casos, sem isolante térmico e com isolante térmico...
Ou seja, basicamente no primeiro caso teremos somente um fluxo de calor interno que será transferido para o ambiente por meio de convecção e radiação, de forma direta.
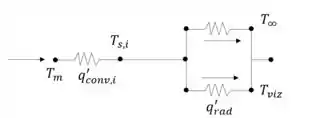
No segundo caso, por termos um isolante térmico, o mesmo fluxo terá primeiro uma convecção interna seguido de uma condução, e por fim, será transferido para o ambiente por meio de convecção e radiação.
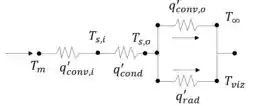
Passo 3
Muito bem, agora podemos partir para a formulação. Mas antes disso notemos que há duas temperaturas muito importantes que não conhecemos, ou seja, e .
Logo, já precisamos ter em mente que iremos cair em uma equação que só será possível através de análise numérica, ou por tentativa e erro...
Passo 4
Vamos lá...
Para resolvermos a questão , basta realizarmos o equacionamento levando em conta o circuito térmico.
Lembrando que não há condução, pois o enunciado nos diz que a parede é delgada, e podemos anular a condução, ou seja, ficará assim:
Note que precisamos determinar os coeficientes de convecção, interno e externo.
Portanto, a partir daqui devemos identificar como se encontra o fluxo no meio e escolher uma correlação para o cálculo do número de Nusselt, e por fim, os coeficientes.
Passo 5
Determinando o fluxo interno:
Como o para escoamento interno, nosso fluxo é turbulento e a correlação correspondente que iremos utilizar é a de Dittus-Boelter, apesar que também poderia se utilizar a de colburn:
Onde para resfriamento, pois nosso duto não está exposto a nenhum meio de aquecimento.
Logo,
Passo 6
No meio externo, temos a presença de convecção natural, logo devemos calcular o Rayleigh:
Note que nosso cilindro pode ser considerado como um cilindro longo, e muito provavelmente ele está na posição horizontal, logo a correlação será:
Logo,
Passo 7
Muito bem, agora que determinamos os coeficientes de convecção, voltaremos a nossa equação inicial:
Realizando a substituição:
Como esperado, chegamos em uma equação que só será resolvida através de analise numérica ou tentativa e erro.
Logo, para terminamos o exercício irei mostrar o resultado:
Portanto, para sabermos a perda de calor por unidade de comprimento do duto, do nosso circuito térmico podemos simplesmente escolher o trecho:
Note que todo calor que entra, é igual ao que sai.
Passo 8
Por fim, para o cálculo da questão :
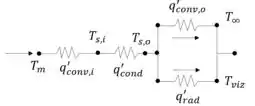
Note que, basta igualarmos o calor transferido por convecção interna ao calor transferido por condução. Visto que todo calor que entra é igual ao que sai.
E
Note que, mais uma vez chegamos em uma equação que só será determinado por análise numérica, ou tentativa e erro. Porém agora teremos que determinar duas temperaturas desconhecidas.
Resposta
A resposta se encontra nos passos anteriores, por se tratar de uma questão especial.