Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 21

Um manômetro é construído com um tubo de vidro de diâmetro interno uniforme, D = 6,35 mm, conforme mostrado na figura. O tubo em U é preenchido parcialmente com água. Em seguida, um volume   = 3,25 cm3 de óleo Meriam vermelho é adicionado no lado esquerdo do tubo. Calcule a altura de equilíbrio, H, quando ambas as pernas do tubo em U estão abertas para a atmosfera..

Passo 1

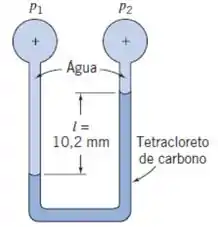
Fala aí galera, vamos para mais um problema de mecânica dos fluidos. Para obtermos a diferença de pressão, temos:

d p d h = ρ g

Temos também que a densidade relativa é dada por:

ρ = S G ∙ ρ á g u a

A partir da equação manométrica do sistema do ponto 1 para o ponto 2, temos: p 2 - P 1 = ρ g ( h 2 - h 1 )

p B - p A = ρ ó l e o ∙ g L

p D - p C = ρ H 2 O ∙ g L - H

Sendo p A = p C = p a t m e p B = p D , temos:

ρ ó l e o g L = ρ H 2 O g L - H S G ó l e o L = L - H H = L 1 - S G ó l e o

Para encontrarmos L :

V ó l e o = π 4 D 2 L L = 4 × 3,25   c m 3 π 6,3 , 5   m m 2 10   m m c m 3 L = 102,62   m m

Por último, vamos calcular o valor de H , dado por:

H = 102,62   m m 1 - 0,827 H = 17,75   m m

Vale ressaltar que o nosso foco não é nas operações matemáticas e sim na nossa MecFlu.

Resposta

L = 102,62   m m

H = 17,75   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O método tradicional para medir a pressão sanguínea usa um esfigmomanômetro, que registra primeiro a pressão mais alta e depois a pressão mais baixa da qual se pode ouvir o ruído “Kortkoff” de escoame
Conduza o seguinte experimento para ilustrar a pressão do ar. Encontre uma régua fina de madeira (de aproximadamente 30 cm de comprimento) ou uma espátula de pintura de madeira fina. Coloque-a na extr
A partir da figura abaixo, determine a pressão manométrica no ponto A em Pa. Ela é mais alta ou mais baixa do que a pressão atmosférica?
O sistema da figura a seguir está a 20°C. Calcule a pressão absoluta no ponto A em Pa.
Um tanque cheio com óleo (d = 0,85) tem 7 m de comprimento e 3 m de profundidade e tem uma seção transversal trapezoidal com 2 m de largura no fundo e 4 m de largura no topo. Calcule (a) o peso do óle