Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas - Ex. 159

O manômetro de três ramos da Figura P2.159 é preenchido com água até uma profundidade de 20   c m . Todos os tubos são longos e têm diâmetros pequenos. Se o sistema gira a uma velocidade angular Ω em torno do tubo central, (a) deduza uma fórmula para encontrar a variação em altura nos tubos; (b) determine a altura em cm em cada tubo se Ω = 120   r p m . (Dica: O tubo central tem de fornecer água para ambos os tubos externos.)

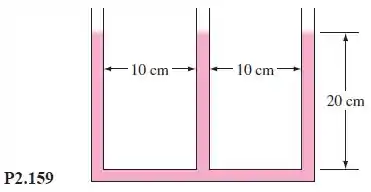
Passo 1

Fala pessoal!! Vem comigo resolver mais uma questão!!

Nessa questão, nós queremos deduzir uma fórmula para encontrar a variação em altura nos tubos para a configuração descrita. Também queremos determine a altura em c m em cada tubo se Ω = 120   r p m .

Passo 2

(a) Para resolver essa questão, podemos fazer o seguinte esquema para a rotação do tubo:

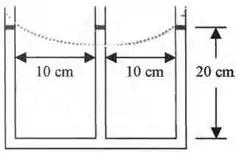
Podemos visualizar no esquema acima que a superfície livre durante a rotação é exemplificada pela linha tracejada. As pernas externas direita e esquerda experimentam um aumento que é metade daquele da perna central, ou

Δ h O = Δ h C 2

O deslocamento total entre os meniscos externos e centrais exemplificado pela Fig. 2.23 é dado por:

Ω 2 R 2 2 g

O menisco central cai dois terços dessa quantidade e alimenta os tubos externos, em que cada um sobe um terço dessa quantidade acima da posição de repouso:

Δ h e x t e r n o = 1 3 Δ h t o t a l = Ω 2 R 2 6 g

Δ h c e n t r o = - 2 3 Δ h t o t a l = - Ω 2 R 2 3 g

Passo 3

(b) Para o caso particular com R = 10   c m e Ω = 120   r p m = 12,57   r a d / s , temos que a altura em cada tudo será:

Δ h t o t a l = 12,57 2 10 2 6 9,81 = 0,0805   m

Δ h e x t e r n o = 1 3 Δ h t o t a l = 1 3 0,0805   m = 0,027   m

Δ h c e n t r o = - 2 3 Δ h t o t a l = - 2 3 0,0805   m = - 0,054   m

Resposta

Δ h e x t e r n o = Ω 2 R 2 6 g

Δ h c e n t r o = - Ω 2 R 2 3 g

Δ h e x t e r n o = 0,027   m

Δ h c e n t r o = - 0,054   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tanque fechado, com a forma indicada na figura, com 0,6m de lado, gira em torno de um eixo com rotação n = 100r p m e a uma distância radial de 1,5m . Qual é a pressão nos pontos A , B e C ? ( ρ =
Determinar a diferença de pressão entre dois pontos genéricos de um tanque cheio de água acelerado verticalmente para cima com uma aceleração a y = 5g .
Um veículo carrega um recipiente que contém água, movimentando-se com uma velocidade constante de 72k m / h . Calcular o tempo mínimo de frenagem com desaceleração constante para que a água não transb
Um acelerômetro é constituído de um tanque e de um manômetro metálico, como indica a figura. Adiciona-se mercúrio no tubo até que a leitura no manômetro seja 175k P a . Dados: γ H g = 136000N / m 3 ;
Um tubo em U contendo água é montado num carro de corrida. O carro parte com aceleração constante e 5s após a partida a água no tubo em U apresenta a configuração indicada. Sendo g = 9,8m / s 2 ;Qual