Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 2.Problemas Abrangentes - Ex. 2
Um malandro colocou óleo, de densidade , no ramo esquerdo do manômetro da Figura PQ2.2. Não obstante, o tubo em U ainda é útil como um dispositivo de medida de pressão. Ele é ligado a um reservatório pressurizado, como mostra a figura.
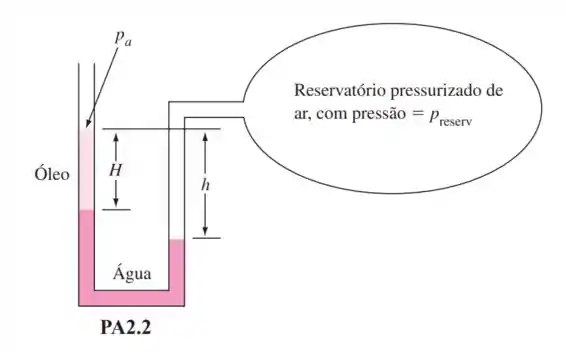
- Encontre uma expressão para em função de e outros parâmetros no problema;
- Encontre o caso especial do seu resultado em quando .
- Admita que , seja 101,2 kPa, seja mais alta do que e . Calcule em cm desprezando os efeitos da tensão superficial e da densidade do ar.
Passo 1
Faaalaaaa clóviiiss!! Mais uma questãozinha de MecFlu e sem desespero, o RA ta aqui pra você! Vamos juntos! Bora!!
Você já deve ta cansado desse esqueminha... mas é com ele mesmo, ponto lá, ponto cá e eles têm a mesma pressão.
Então vamos começar com o ponto do lado esquerdo, quem é esse cara?
Enquanto que do outro lado teremos:
Mas aí você pode estar pensando, “Cara, e aquela coluna de ar que tá ali??”
Boa, mostra que você tá muito por dentro do assunto. Mas o enunciado disse que podemos desconsiderar os efeitos da densidade do ar, o que significa que a gente pode desconsiderar a ação dessa coluna.
Simples, não?
Passo 2
Eles estão no mesmo nível, logo podemos dizer que essas duas pressões são iguais:
Como queremos isolar , basta brincar com essa expressão, e vamos chegar em algo assim:
Dando uma arrumada:
Temos então essa nossa primeira resposta.
Para a alternativa (b), é só adotarmos , e portanto
Bem tranquilo!
Passo 3
E na letra (c) sem maiores delongas, basta substituirmos os valores dados.
Note que, .
E considerando: e também que:
Finalmente:
E então:
Como o exercício pede em :
E isso é tudo!!
Resposta
Portanto: