Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 2.Exercício - Ex. 54

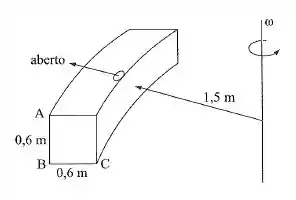
Um tanque fechado, com a forma indicada na figura, com 0,6   m de lado, gira em torno de um eixo com rotação n = 100   r p m e a uma distância radial de 1,5   m . Qual é a pressão nos pontos A , B e C ? ( ρ = 1000   k g / m 3 ; p a t m = 100   k P a )

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para resolver este exercício iremos utilizar a equação abaixo que representa a variação de pressão entre dois pontos quaisquer:

p 3 - p 1 = r ω 2 2 ∆ r 3,1 2 - γ ∆ z 3,1

Para encontrar a pressão nos pontos pedidos basta utilizar a equação acima. No ponto A podemos perceber que a pressão será a pressão atmosférica mais a pressão relativa à distância.

Já no ponto B , será a pressão em A mais a pressão relativa ao deslocamento vertical para baixo. E em C , será a pressão atmosférica mais a pressão relativa ao deslocamento vertical. Lembrando que fora do tanque a pressão é atmosférica:

p A = r ω 2 2 ∆ r 2 + p a t m - γ ∆ z

p A = 1000 10,5 2 2 0,6 2 + 10 5 - γ 0

p A = 119,7   k P a

Passo 2

No ponto B , temos que:

p B = p A + ρ g h

p B = 119,7 ⋅ 10 3 + 1000 10 0,6

p B = 125,7   k P a

No ponto C , temos que:

p C = p a t m + ρ g h

p C = 100 ⋅ 10 3 + 1000 10 0,6

p C = 106   k P a

Resposta

p A = 119,7   k P a

p B = 125,7   k P a

p C = 106   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um acelerômetro rudimentar pode ser feito com um tubo em U cheio de líquido, conforme mostrado. Deduza uma expressão para a diferença de nível h, causada por uma aceleração , em termos, da geometria d
Um contêiner cilíndrico, semelhante ao analisado no Exemplo 3.10 (no site da LTC Editora), é girado a uma velocidade angular constante de 2 Hz em torno do seu eixo. O cilindro tem 0,5 m de diâmetro e
Centrífugas de gás são usadas em um processo de produção de urânio enriquecido para varetas de combustível nuclear. A velocidade periférica máxima de um gás nessas centrífugas é limitada, por consider
Um balde cilíndrico, com diâmetro e altura de 400m m , pesa 15 N e contém água até uma altura de 200 mm. O balde é girado a 5m / s em uma trajetória circular vertical de raio igual a 1 m. Suponha que
Um tubo de ensaio é girado em uma centrifuga. O suporte do tubo é montado em um pivô de modo que o tubo báscula para fora à medida que a rotação aumenta. Para altas velocidades, o tubo fica aproximada