Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 104
Se a massa M no Problema 3.101 for liberada do tirante, quanto do tirante permanecerá submerso na nova condição de equilíbrio? Qual será a força mínima para cima necessária para levantar a extremidade do tirante até imediatamente fora d’água?
Passo 1
Tomando como base o problema 101, temos a geometria da haste. Devemos encontrar quanto da parte ficará submersa e qual será a força para levantar a mesma.
A seguir temos o diagrama que representa o problema:
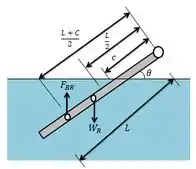
Podemos analisar as forças:
Vamos chamar de a força de flutuabilidade da haste,logo,
Sendo que e , podemos substituir na equação:
Passo 2
A equação que formamos no Passo 1, podemos isolar em relação a :
Substituindo os dados:
Então, a quantidade do tirante que permanecerá submerso é .
Levantar a haste da água exige uma força igual à metade do peso da haste (a reação também leva a metade do peso)
Passo 3
Agora para encontrarmos a foça necessária para levantar o tirante, temos a analise de que a força precisa ser igual a metade do peso do objeto:
Prontinho!!