Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 100
Um balão de hélio deve elevar uma carga a uma altitude de 40 km, onde a pressão e a temperatura atmosféricas são respectivamente 3,0 mbar e –25ºC. O material do balão é poliéster com densidade relativa de 1,28 e espessura de 0,015 mm. Para manter uma forma esférica, o balão é pressurizado até uma pressão manométrica de 0,45 mbar. Determine o diâmetro máximo do balão, se a tensão máxima admissível no tecido está limitada a 62 MN/m2. Que carga pode ser transportada?
Passo 1
Temos aqui um balão pressurizado que deve ser projetado para elevar uma carga útil de massa a uma altitude de , onde e . A pele do balão tem uma gravidade específica de e espessura de . A pressão manométrica é de . A tensão de tração permitida no balão é de .
Assim, vamos encontrar o diâmetro máximo do balão e a massa máxima da carga útil. Para isso, aplicaremos as equações hidrostáticas neste sistema:
(a força de empuxo é igual à massa de fluido deslocado)
(Equação de estado ideal dos gases)
Faremos as seguintes considerações: fluido estático e incompressível, equilíbrio estático a de altitude, e comportamento ideal do gás.
Passo 2
O diâmetro do balão é limitado pela tensão elástica permitido na pele:
Resolvendo esta expressão para o diâmetro:
Para encontrar a carga útil máxima permitida, fazemos a relação entre as forças segundo o diagrama:
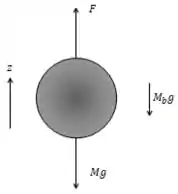
Isolando para :
Sabendo que o volume do balão é: . O volume da pele é: . Então:
A densidade do ar é:
E a do Hélio:
Então a massa é:
Prontinho!!