Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 3.Problemas - Ex. 107
Uma tora cilíndrica, com D = 0,3 m e L = 4 m, é mais pesada na sua extremidade inferior, de modo que flutua verticalmente com 3 m submersos na água. Quando deslocada verticalmente da sua posição de equilíbrio, a tora oscila ou “saltita” na direção vertical ao ser solta. Estime a frequência de oscilação da tora. Despreze efeitos viscosos e o movimento da água.
Passo 1
Temos nesse problema uma madeira cilíndrica, com as dimensões dadas no enunciado, é pesada na extremidade inferior, de modo que flutua verticalmente com
submersos na água do mar. Quando deslocada verticalmente do equilíbrio, a tora oscila na direção vertical após a liberação.
Devemos estimar a frequência da oscilação. Para isso, fazemos algumas considerações: fluido estático e incompressível; pressão atmosférica atuando em todos os lugares; efeitos viscosos e movimento da água são insignificantes.
Aplicaremos a seguinte equação hidrostática:
(a força de empuxo é igual ao peso do fluido deslocado)
Passo 2
Para começarmos a resolver temos o seguinte diagrama de corpo livre:
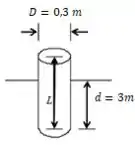
No equilíbrio, temos:
Onde . Assim, quando a madeira se desloca, temos:
Substituindo alguns dados:
Logo,
Temos a E.D.O:
Passo 3
Essa E.D.O, descreve um movimento harmônico simples com a frequência natural descrita por:
Para expressar a frequência, temos:
Prontinho!!