Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 99

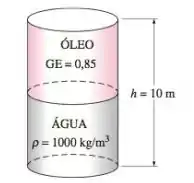
A metade inferior de um contêiner cilíndrico com 10   m de altura é preenchida com água ( ρ = 1000   k g / m 3 ) e a metade superior com óleo que tem gravidade específica de 0,85 . Determine a diferença de pressão entre a parte superior e inferior do cilindro.

Passo 1

Fala aí galera, bora fazer mais uma questão de MecFlu. Primeiramente, temos que a densidade do óleo é obtida multiplicando sua densidade específica gravidade pela densidade da água. temos:

ρ ó l e o = S G × ρ H 2 O = 0,85 1000 ρ ó l e o = 850   k g / m 3

Com isso, a diferença de pressão entre a parte superior e a parte inferior do cilindro é a soma das diferenças de pressão nos dois fluidos, logo:

∆ P t o t a l = ∆ P ó l e o + ∆ P H 2 O   ∆ P t o t a l = ρ g h ó l e o + ρ g h H 2 O ∆ P t o t a l = 850 k g m 3 9,81 m s 2 5   m + 100 0 k g m 3 9,81 m s 2 5   m ∆ P t o t a l = 90,7   k P a

Resposta

∆ P t o t a l = 90,7   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ao medir diferenças de pressão pequenas com um manômetro, quase sempre um braço do manômetro é inclinado para melhorar a exatidão da leitura. (A diferença de pressão ainda é proporcional à distância v
Defina a força hidrostática resultante que age em uma superfície submersa e o centro da pressão.
Uma pedra de granito de 170k g ( ρ = 2.700k g / m 3 ) é solta em um lago. Um homem mergulha e tenta erguer a pedra. Determine quanta força o homem precisa aplicar para levantá-la do fundo do lago. Voc
Uma placa plana horizontal submersa é suspensa na água por uma corda anexada ao centróide de sua superfície superior. Agora a placa é girada a 45 ° com relação a um eixo que passa através de seu centr
Uma pessoa diz que pode determinar a intensidade da força hidrostática que age sobre uma superfície plana submersa na água, independente da forma e orientação, se ela conhecer a distância vertical do