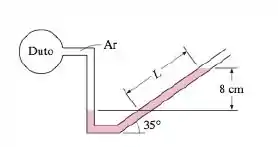
Ao medir diferenças de pressão pequenas com um manômetro, quase sempre um braço do manômetro é inclinado para melhorar a exatidão da leitura. (A diferença de pressão ainda é proporcional à distância vertical, e não ao comprimento real do fluido ao longo do tubo). A pressão do ar em um duto circular deve ser medida usando-se um manômetro cujo braço aberto está inclinado a da horizontal, como mostra a figura. A densidade do líquido é de , e a distância vertical entre os níveis de fluido dos dois braços do manômetro é de Determine a pressão manométrica do ar no duto e o comprimento da coluna de fluido no braço inclinado acima do nível do fluido no braço vertical.

Fala aí galerinha do responde aí, bora garantir aquele notão em Mecflu. Primeiramente, como líquidos na mesma altura possuem a mesma pressão, a pressão do ar no duto tem que ser igual a pressão exercida pelo braço acima da linha horizontal. Logo, como a seção do tubo é constante:

Considerando e em

Para calcular o tamanho do braço inclinado, temos que usar as relações do triângulo retângulo formado pelo tubo, a altura de e a linha horizontal. Portanto: