Um método extremamente efetivo para resfriar circuitos integrados de silício com elevada densidade de potência envolve a gravação de microcanais na superfície inferior (sem circuitos) do chip. Os canais são cobertos por uma cobertura de silício e o resfriamento é mantido através da passagem de água pelos canais.

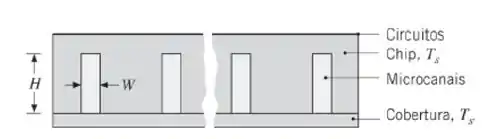
Seja um chip com 10 mm × 10 mm de lado no qual foram gravados cinquenta microcanais retangulares com 10 mm de comprimento, cada um com largura W = 50 μm e altura H = 200 μm. Considere condições operacionais nas quais água entra em cada microcanal a uma temperatura de 290 K e a uma vazão de kg/s, enquanto o chip e a cobertura se encontram a uma temperatura uniforme de 350 K. Considerando escoamento plenamente desenvolvido nos canais e que todo o calor dissipado pelos circuitos seja transferido para a água, determine a

temperatura de saída da água e a potência dissipada pelo chip. As propriedades da água podem ser estimadas a 300 K.

Com o número de Reynolds encontrado no passo 1, temos que o escoamento é laminar. Com isso, vamos consultar a tabela 8.1 vista nessa seção e apresentada a seguir para obter no número de Nusselt para o escoamento:

Então, precisamos calcular a razão b/a, onde teremos:

E, como temos uniforme, então no nosso caso teremos:

Com isso, sabendo que o número de Nusselt se relaciona com o coeficiente convectivo através da seguinte relação:

Substituindo os valores conhecidos, temos:

Agora, como no nosso caso temos constante, iremos utilizar a equação 8.41b vista nesse capítulo, onde temos:

Sabendo que o perímetro é dado por:

Então, substituindo os valores conhecidos na equação de cima, chegaremos em:

Agora, com a temperatura de saída, conseguimos encontrar a potência dissipada pelo chip, através do calor trocado com a água, dada por:

Substituindo os valores conhecidos, temos: