Um gás ideal escoa no interior de um tubo de pequeno diâmetro. Deduza uma expressão para a densidade (massa específica) de transição do gás, , abaixo da qual os efeitos de microescala têm que ser levados em conta. Expresse os seus resultados em termos do diâmetro da molécula do gás, da constante universal dos gases, da constante de Boltzmann e do diâmetro do tubo. Avalie a densidade de transição para um tubo com diâmetro D = 10 μm, para o hidrogênio, o ar e o dióxido de carbono. Compare as densidades de transição calculadas com as densidades dos gases à pressão atmosférica e T = 23 °C.
Passo 1
Beleza, a primeira coisa que devemos fazer é pegar algumas propriedades dos gases à pressão atmosférica e a 23 °C = 300 K. Faremos isso consultando a tabela A.4 do apêndice A, onde teremos, para o ar:
Agora para o hidrogênio, teremos:
Para o dióxido de carbono:
Agora, nós vamos recorrer à figura 2.8 vista no capítulo 2, onde poderemos pegar os valores dos diâmetros moleculares, então temos:
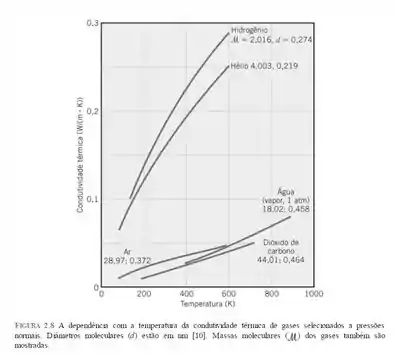
Com ela, podemos extrair os seguintes diâmetros moleculares:
Passo 2
Agora nós vamos recorrer à equação do livre percurso médio, dado pela equação 2.11, onde temos:
Sabemos que a pressão pode ser escrita em função da equação do gás ideal, dada por:
Substituindo essa expresão na equação para o livre percurso médio, temos:
Sabemos que os efeitos de microescala se tornam importante a partir de:
Então, dividindo a equação para o livre percurso médio por dos dois lados, podemos escrever:
Então, de acordo com a relação anteriormente, temos:
Isolando a densidade de transição do gás temos:
Então, sabendo que a constante de Boltzmann é , substituindo os valores conhecidos nessa equação para o ar, chegamos em:
Passo 3
Agora, repetindo os cálculos do passo 2 para o hidrogênio, teremos:
E, para o gás carbônico, teremos:
Agora nós vamos comparar essas densidades com aquelas lá do passo 1 a 1 atm e 300 K, então, para o ar, temos:
Repetindo os cálculos para o hidrogênio e para o gás carbônico, teremos: