Um método para produzir finas lâminas de silício para uso em painéis solares fotovoltaicos é passar, de baixo para cima, duas fitas finas de material com alta temperatura de fusão através de um banho de silício líquido. O silício se solidifica sobre as fitas próximo à superfície do líquido fundido e as lâminas sólidas de silício são puxadas vagarosamente para fora do líquido. O silício é reabastecido através da adição de pó sólido de silício que é jogado no banho. Considere uma lâmina de silício, que tem largura e espessura , sendo puxada para fora do banho a uma velocidade de . O silício é fundido através do suprimento de potência elétrica à câmara cilíndrica de produção, com altura e diâmetro . As superfícies expostas da câmara de produção estão a , o coeficiente convectivo correspondente nas superfícies expostas é e a superfície é caracterizada por uma emissividade igual a . O pó sólido de silício está a e a lâmina sólida de silício deixa a câmara a . As temperaturas de vizinhança e do ambiente são .

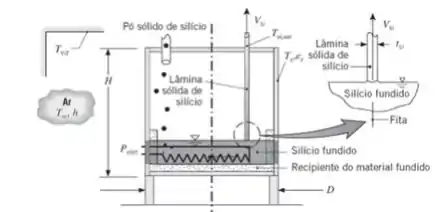
a) Determine a potência elétrico, , necessária para operar o sistema em regime estacionário.

b) Se o painel fotovoltaico absorver um fluxo solar médio no tempo de e o painel tiver uma eficiência de conversão (razão entre a potência elétrica produzida e a potência solar absorvida) de ; quanto tempo o painel solar deve operar para produzir energia elétrica suficiente para compensar a energia elétrica consumida na sua fabricação?

Letra a)

Resolvendo a questão, calcularemos a vazão mássica do silício que sai da câmara:

Dados:

;

;

.

Temos:

Seguindo, calcularemos a área total da superfície:

Sendo:

;

.

Temos:

Agora, analisaremos o balanço de energia:

A partir do balanço estendido, conseguimos obter .

Dados:

;

;

;

;

;

;

;

;

;

;

;

.

Temos:

Letra b)

Para a segunda parte da questão, calcularemos de início a energia elétrica produzida pelo painel:

Com:

;

;

Temos:

Agora, calcularemos a área do painel solar necessária para o desenvolvimento da energia elétrica suficiente consumida:

Substituindo os dados:

Calculando a área da lâmina produzida por minuto:

Dados:

;

.

Temos:

Por fim, obteremos o tempo necessário para o painel solar ser operado para produzir energia elétrica suficiente.