Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 15.Problemas - Ex. 36
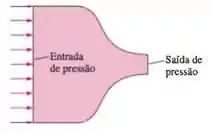
Gere um domínio computacional para estudar o escoamento compressível do ar através de um bocal convergente com pressão atmosférica na saída do bocal (Figura PI 5-36). As paredes do bocal podem ser aproximadas como não viscosas (tensão de cisalhamento zero). Execute vários casos com diversos valores de pressão de entrada. Quanta pressão de entrada é necessária para estrangular o escoamento? O que acontece se a pressão de entrada é mais alta do que esse valor? Discuta.
Passo 1
Fala aí, galerinha. Tudo beleza? Vamos fazer mais uma questão de MecFlu pra tirar aquele na prova. Neste problema devemos gerar soluções CFD para vários comprimentos de extensão de tubo a jusante para ver o impacto do limite a jusante. Também devemos discutir a variação de com .
Temos que o fluxo é constante e incompressível, assimétrico em relação ao eixo e laminar.
As propriedades da água são:
Apenas o primeiro caso em tem fluxo reverso na saída de pressão. Por , os problemas de fluxo reverso desapareceram. As linhas de fluxo revelam que o fluxo se separa no canto, formando um redemoinho recirculante. O redemoinho se reconecta em aproximadamente .
As linhas aerodinâmicas são mostradas para os três primeiros casos abaixo:
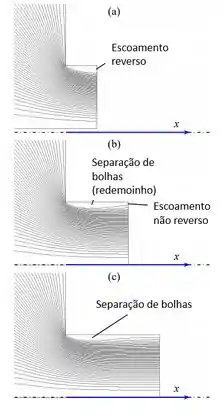
As formas gerais das linhas aeradas parecem não ser afetadas pela extensão a jusante do domínio computacional
Passo 2
Em seguida, temos que , e são tabulados como funções de é independente de (até três dígitos significativos de precisão) por . Portanto, o pino de pressão manométrica de entrada é plotado como uma função de :
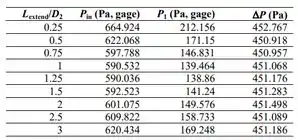
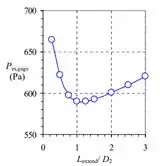
Asssim, a pressão de entrada cai conforme aumenta de para , e então começa a aumentar lentamente conforme continua a aumentar. Explicamos essa tendência com a ajuda das linhas de fluxo no primeiro passo.
Em primeiro lugar, os dados para não são confiáveis, pois há fluxo reverso na saída de pressão. Assim, começamos nossa discussão em . A bolha de separação (redemoinho recirculante) na entrada do tubo de menor diâmetro força o fluxo a convergir e acelerar através de uma área efetiva que é menor do que a área da seção transversal do tubo pequeno (uma vena contracta). Este fluxo de alta velocidade leva a uma região de baixa pressão perto da bolha de separação.
A jusante da bolha de separação, a pressão tenta aumentar ligeiramente (a porção a jusante do redemoinho se comporta como um difusor, recuperando parte da perda de pressão). No entanto, uma vez que a pressão de saída é fixada em pressão manométrica zero, a pressão de entrada deve diminuir para compensar. Isso explica por que diminui quando aumenta de para . Por , a saída do domínio computacional está além da região de recuperação de pressão devido ao redemoinho, e o fluxo começa seu lento desenvolvimento em direção ao fluxo laminar totalmente desenvolvido. Além de , a pressão diminui fluxo reversoaxialmente ao longo do tubo devido ao atrito ao longo da parede do tubo. Mas como a pressão de saída é atmosférica, a pressão de entrada
deve subir em conformidade. Em outras palavras, a pressão na entrada deve aumentar para superar a queda de pressão crescente através do tubo. Esperamos que essa tendência continue, eventualmente se tornando linear.
Com base em todos os nossos resultados coletados, recomendamos que Shane use um valor de para ou mais para garantir a simulação adequada deste fluxo. Se a velocidade do computador ou a memória for um problema, ele pode escapar com um mínimo de para evitar problemas de fluxo reverso na saída.
É isso, galera. Bora pra praticar mais pra ficar craque.
Resposta
para ou mais