Um modelo de um moinho de vento de pás múltiplas, típico de fazenda americana, deve ser construído para demonstração. O modelo, com D = 1m , deve desenvolver potência máxima a uma velocidade do vento de V = 10m / s . Calcule a velocidade angular do modelo para ótima geração de potência. Estime a potência produzida.

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 10.Problemas - Ex. 113

Um modelo de um moinho de vento de pás múltiplas, típico de fazenda americana, deve ser construído para demonstração. O modelo, com , deve desenvolver potência máxima a uma velocidade do vento de . Calcule a velocidade angular do modelo para ótima geração de potência. Estime a potência produzida.

Passo 1

Tá legal! Vamos começar o exercício encontrando o valor do coeficiente de potência e da razão de velocidade periférica da turbina através da Figura 10.50 dessa seção:

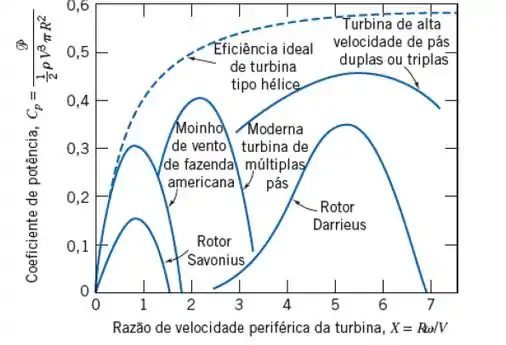
Então, como no nosso caso temos um moinho de vento, o coeficiente de potência para a eficiência máxima será:

E a razão correspondente será:

Passo 2

Agora, vamos utilizar a equação da razão de velocidade periférica da turbina para encontrar a velocidade angular do moinho:

Substituindo os valores conhecidos:

Convertendo esse valor para , temos:

Passo 3

Agora, a partir do coeficiente de potência para o sistema, podemos encontrar a potência total fornecida ao sistema:

Substituindo os valores conhecidos, temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A turbina para um novo motor a jato foi projetado para condições de entrada de 1100 kPa e 925°C, recebendo 250 Kg/s a velocidade de 500 rpm e condições de saída de 550 kPa e 730°C. Se a altitude e o c

A eficiência de propulsão, η , de uma hélice é definida como a razão entre o trabalho útil produzido e a energia mecânica cedida ao fluido. Determine a eficiência de propulsão do barco em movimento do

Um moinho típico de fazenda americana, com pás múltiplas, tem D = 2,1m e foi projetado para produzir potência máxima em ventos com V = 24k m / h . Estime a vazão de água fornecida como função da altur

Escreva a velocidade específica da bomba em termos do coeficiente de vazão e do coeficiente de carga.