Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 2.Problemas - Ex. 101
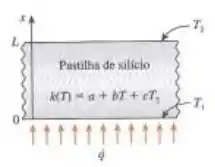
Uma pastilha de silício com espessura de é aquecida com um fluxo de calor uniforme na superfície inferior. A pastilha de silício tem uma condutividade térmica que varia com a temperatura e pode ser expressa como , onde , e . Para evitar a deformação, a diferença de temperatura na espessura da pastilha não pode exceder 2 °C. Considerando que a superfície superior da pastilha de silício está na temperatura uniforme de 600 K, determine o máximo permitido de fluxo de calor.
Passo 1
O nosso primeiro passo é fazer considerações para resolver o nosso problema. Sendo assim, temos um problema de regime permanente, com condução de calor unidimensional, geração de calor, mas a condutividade térmica não é constante.
Como estamos trabalhando com uma placa, vamos utilizar o sistema de coordenadas retangular. Como queremos determinar o fluxo de calor, precisamos resolver a seguinte equação:
Temos uma EDO. E agora? Nosso primeiro passo é substituir a função condutividade térmica. Com isto, temos:
Passo 2
Agora, nosso papel é tentar resolver a EDO obtida no passo anterior. Ela é uma EDO de primeira ordem separável. Portanto, vamos separar os termos e e integrar a nossa equação. Sendo assim,
Observem que os limites de integração correspondem aos limites físicos da nossa pastilha. Integrando, temos:
Quase lá! Saber quem é , pois a questão nos informa quem é . Como a diferença entre as temperaturas das superfícies não deve ultrapassar o valor de 2 °C, então, automaticamente, é igual a 602 °C ou 598 °C. Temos 50% de chance agora!
E o que utilizaremos para identificar? Simples! Vamos usar o desenho da questão! Observem o sentido do fluxo de calor. Ele vai da maior temperatura para a menor temperatura! Portanto, a maior temperatura é na superfície de baixo . Logo, . Agora sim, substituindo todos os valores na nossa equação, temos:
E chegamos a nossa solução.