63 – Reconsidere o Prob. 2-16. Usando a relação obtida para a variação da temperatura da placa da base do ferro, trace a temperatura como função da distância no intervalo de a e discuta os resultados. Use EES (ou outro programa).
Passo 1
a)
Encontre o fluxo de calor através da superfície interna usando a equação. (Como a parte superior do ferro é bem isolada e, portanto, todo o calor gerado nos fios de resistência é transferido para a placa de base)
Aqui, é a capacidade de ferro e é a área base da chapa
Substitua 800 W por e para .
Passo 2
Tome a direção normal da superfície da parede como sendo a direção x com x = 0 na superfície interna e escreva que a formulação matemática desse problema pode ser expressa da seguinte forma:
A primeira condição de contorno está na superfície interna da placa de base, sujeita a um fluxo de calor uniforme e é devido à condução de calor
Aqui, é a condutividade térmica da placa.
E a segunda condição de contorno está na temperatura da superfície externa da placa de base,
Em , a temperatura da superfície externa é
Passo 3
Considere a equação matemática para encontrar a variação de temperatura,
Integre a equação diferencial duas vezes em relação a .
…… (1)
…… (2)
Aqui e são constantes arbitrárias.
Encontre as constantes aplicando as condições de contorno,
Aplique a primeira condição de contorno, em
Considere a equação (1) e substitua por
Aplique a segunda condição de contorno para calcular o valor constante
Substitua os valores conhecidos na equação (2).
Substitua e na equação geral da distribuição de temperatura,
Substituir por e para .
Portanto, a variação de temperatura na placa de base é
Agora tabule os valores da temperatura em diferentes valores de x de 0 a 0,6 cm, como mostrado abaixo:
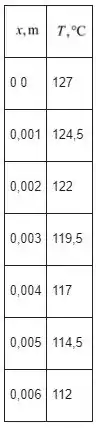
Passo 4
Agora plote o gráfico que mostra a variação de temperatura em função da espessura
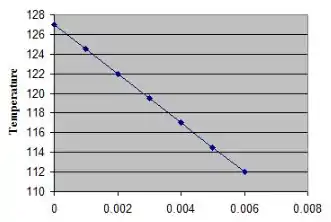
A partir do gráfico, observa-se que, à medida que a condutividade térmica aumenta, a taxa de transferência de calor diminui.
Resposta
A partir do gráfico, observa-se que, à medida que a condutividade térmica aumenta, a taxa de transferência de calor diminui.