Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 122
Uma placa de circuito impresso de 0,4 cm de espessura, 12 cm de altura e 18 cm de comprimento contém em um lado 80 chips lógicos estreitamente espaçados, cada um dissipando 0,04 W. A placa está impregnada com recheios de cobre e tem condutividade térmica efetiva de . Todo o calor gerado nos chips é conduzido através da placa de circuito e é dissipado a partir do verso da placa para o meio a 40°C, com um coeficiente de transferência de calor de 52 .
- Determine as temperaturas dos dois lados da placa de circuito.
- Agora, uma chapa de alumínio de 0,2 cm de espessura, 12 cm de altura e 18 cm de comprimento com 864 aletas de pino de alumínio de 2 cm de comprimento e 0,25 cm é fixada no lado de trás da placa de circuito impresso com adesivo epóxi de 0,02 cm de espessura. Determine as novas temperaturas sobre os dois lados da placa de circuito.
Passo 1
Boom galera, o que temos aqui??
Nós temos o chip dissipando o calor através da placa do circuito, sendo assim nós temos duas resistências atuando aqui, a resistência à condução da placa e a convectiva, ok?
Então vamos desenhar:
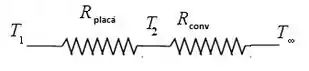
Vamos ver como se calcula?
Já sabemos que:
E quanto a área?
Se nós considerarmos o chip como sendo um retângulo a área será simplesmente a altura vezes o comprimento:
Substituindo:
Agora nós podemos achar as resistências:
Como todas estão em série a resistência total será:
Passo 2
Com a resistência total nós podemos achar qual a taxa que calor atravessa a placa:
Mas esperem aí! Cadê o caloor??
Já temos né, galera !!
Como temos 80 chips dissipando 0,04 W:
Agora é só substituir:
Podemos usar esta mesma relação para achar , mas usaremos aqui somente a resistência da placa:
Substituindo:
E é isso gente!!
Achamos a temperatura dos dois lados da placa!
Passo 3
Agora nós temos o chip dissipando o calor através da placa do circuito, da camada de epóxi, por meio da aleta de alumínio e, por ultimo, a convectiva, ok?
Então vamos desenhar:
A resistência da placa, do epóxi e do alumínio são calculadas igualmente, ok?
A resistência da placa nós já sabemos:
Agora precisamos das demais!
Substituindo na fórmula do passo 1 e sabendo que a área não variou:
Só precisamos da convectiva, mas para calcula-la vai haver um porém!
Nós teremos os pinos trocando calor com o ambiente então precisamos da área total, área aletada mais a área não aletada:
A área não aletada será a área total do chip menos a área ocupada pelos 864 pinos:
Sabendo que o diâmetro dos pinos é 0,0025 m:
Passo 4
A área aletada é um pouco mais complicada para se calcular, vamos ver como:
A única coisa que não temos é a eficiência da aleta, mas podemos calcula-la se considerarmos condições adiabáticas:
Lembrando que:
Como é uma aleta circular:
Substituindo:
Na eficiência:
Agora conseguimos calcular a área:
Bora calcular a área total?
Se nós temos a área total para transferência de calor externa podemos calcular a resistência convectiva externa:
Como todas estão em série a resistência total será:
Passo 5
Com a resistência total nós podemos achar qual a taxa que calor atravessa a placa:
Substituindo:
Podemos usar esta mesma relação para achar , mas usaremos aqui somente a resistência da placa:
Substituindo:
E finalizamos mais uma galerinhaa !!