Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 121
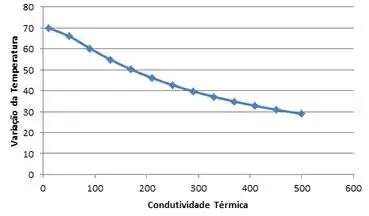
Reconsidere Prob. 3–119. Usando EES (ou outro software), investigue os efeitos da condutividade térmica do material da colher e o comprimento da sua extensão no ar sobre a diferença de temperatura atraves da superfície exposta do cabo da colher. Deixe a condutividade térmica variar de a bem como o comprimento de 10 cm a 30 cm. Plote a diferença de temperatura como funções da condutividade térmica e comprimento, e discuta os resultados.
Passo 1
Preparados ??
Espero que sim !!
Nós já sabemos que algumas coisas permanecerão constantes quando variamos a condutividade térmica do material, certo?
E quais são elas?
Vamos ver:
Se tudo isso permanece constante, o que varia então?
O valor de m depende dessa condutividade e, por isso, também irá variar:
Se o m varia temos o valor da temperatura variando:
E, consequentemente, a variação da temperatura:
Usando o Excel como software:
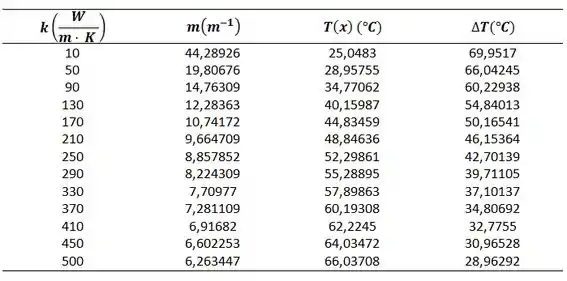
Plotando o gráfico:
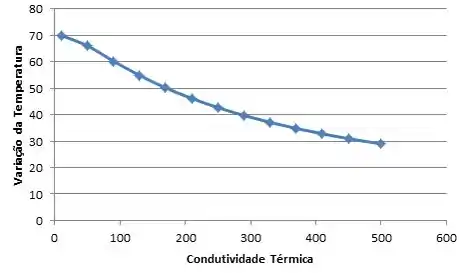
Passo 2
Agora nós vamos variar o comprimento L que não está imersa da colher, bora ver o que não variam então?
Se tudo isso permanece constante, o que varia então?
Somente o valor do cosseno hiperbólico, então temos o valor da temperatura variando:
E, consequentemente, a variação da temperatura:
Usando o Excel como software:
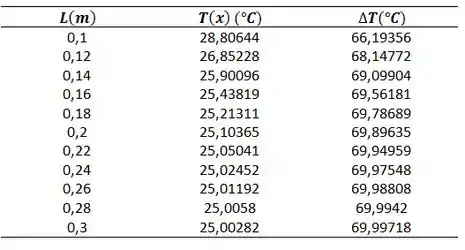
Plotando o gráfico:
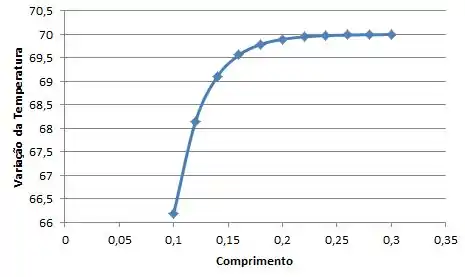
Agora nós concluímos que, à medida que aumentamos o comprimento, aumentamos a diferença de temperatura até atingir um platô, ou seja, a temperatura não vai mais variar. O oposto é observado pela condutividade térmica, quando aumentamos a condutividade térmica nós diminuímos a variação de temperatura, processo que também atinge um platô.
Legal, não foi?
Resposta
