Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 3.Problemas - Ex. 125
Repita o problema 3-124 usando aletas de cobre em vez de alumínio.
Passo 1
Boom galera, antes de qualquer coisa precisamos saber que aqui existem aletas cilíndricas, certo?
Olhando a Tabela 3-3:
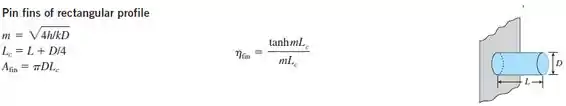
Essa tabelinha é bem importante!!
Agora que já sabemos como calcular parâmetros importantes vamos voltar ao que foi pedido pelo problema, determinar a taxa de transferência de calor a partir da superfície da placa de !
Se queremos a transferência de calor da placa, queremos a transferência que ocorre na parte superfície aletada e na superfície não aletada:
Vamos começar pela troca de calor pelas aletas, ok?
Se lembram como calculamos?
Temos que:
Ainda não temos a área nem a eficiência, certo?
Mas a tabela diz que:
E:
Então:
Se:
Mas calmaa!!
Essa é a área para uma aleta, então vamos precisar descobrir quantas aletas existem nessa placa e aí sim descobrir a área aletada, tudo bem?
Para descobrir vamos dividir a área total pela área de “quadrado vago”, ou seja, sem aleta. Como esse “quadrado vago” tem dois lados iguais de 0,6 cm:
Agora a área total aletada será:
Passo 2
Achamos a área, e agora?
Só falta achar a eficiência, certo?
Então bora lá !!
Olhando a tabela:
E:
Se:
Então:
E a eficiência:
Fechou, galera !
Agora vamos calcular o calor, tudo certo?
Como a variação em graus Celsius e kelvin é a mesma:
Passo 3
Se já achamos a taxa de transferência de calor para a superfície aletada só nos resta achar a taxa para a superfície não aletada.
Sabemos a fórmula?
Claro que sabemos !!
Só nos falta achar aqui a área, certo?
Mas como?
Simples! Basta nós tirarmos a área da seção circular referente às 27777 aletas da área total:
Substituindo:
Na fórmula do calor:
Agora nós temos tudo o que precisamos para achar a troca de calor total:
Ou melhor:
Já acabou?
Não, né! Ainda Falta a eficácia!
Passo 4
Para a eficácia nós temos uma fórmula bem simples:
Já sabemos que:
Mas e quanto ao calor da superfície sem aletas?
Fácil, faremos o mesmo cálculo que fizemos no Passo 3, mas usando a área total, já que aqui não existiriam as aletas:
Substituindo:
Agora sim!!!
Vamos calcular a eficácia:
Finalizamos mais uma !!