A placa de cobertura de um coletor solar plano encontra-se a 15 °C, enquanto ar ambiente a 10 °C escoa paralelamente a sua superfície superior com uma velocidade = 2 m/s.

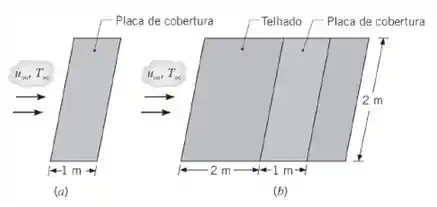
(a) Qual é a taxa de perda de calor por convecção na placa de cobertura?

(b) Se a placa estiver instalada a 2 m da aresta frontal do telhado e encontrar-se alinhada com a sua superfície, qual é a taxa de perda de calor por convecção?

Nós sabemos que o número de Nusselt se relaciona com o coeficiente convectivo através da seguinte equação:

Então, substituindo os valores encontrados no passo 1, temos:

E, sabemos que a equação para o calor trocado por convecção é dada por:

Então, substituindo os valores conhecidos nessa equação, temos:

Agora, para a letra (b) nós vamos calcular o número de Reynolds para o telhado e o coletor, agora com comprimento , então, teremos:

Então, como temos , esse escoamento será laminar, dessa forma, nesse caso, tendo comprimento inicial não aquecido, iremos utilizar a equação 7.42, dada por:

E, a expressão para é dada pela equação 7.23, que será:

Substituindo essa expressão na equação anterior, temos:

E, substituindo a expressão para o número de Reynolds, temos:

Então agora podemos escrever a taxa de transferência de calor em função do comprimento inicial não aquecido, então, teremos:

Sabemos que podemos escrever o coeficiente convectivo em função do Nusselt, então a equação acima se torna:

Precisamos resolver essa integral numericamente, então, substituindo os valores conhecidos e utilizando uma calculadora, chegamos em: