Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 44
Uma série de 10 circuitos integrados (chips) de silício, cada um com comprimento L = 10 mm, é isolada em uma de suas superfícies e resfriada pela superfície oposta com ar atmosférico, em escoamento paralelo, com = 24 °C e = 40 m/s. Quando em operação, a mesma potência elétrica é dissipada em cada chip, mantendo um fluxo térmico uniforme ao longo de toda a superfície resfriada.
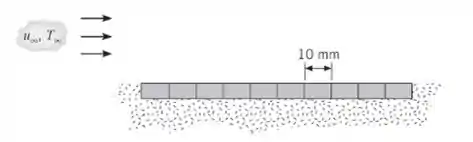
Se a temperatura em cada chip não pode ultrapassar 80 °C, qual é a potência máxima permitida em cada chip? Qual é a potência máxima permitida se um promotor de turbulência for utilizado para perturbar a camada-limite na aresta frontal? Seria preferível orientar a série de chips em uma direção normal ao escoamento do ar ao invés de na direção paralela?
Passo 1
Beleza! Vamos começar esse exercício calculando o valor de , que será:
Então, para essa temperatura, temos as seguintes propriedades para o ar:
Agora nós vamos calcular o número de Reynolds para saber se o escoamento, sem o promotor de turbulência, é laminar ou possui transição para turbulento, então, teremos:
Então, como temos , esse escoamento será laminar ao longo de todos os chips.
Passo 2
Dessa forma, sabemos que o menor coeficiente convectivo local existe no último chip, então é ele que será nosso limitante em questão de potência máxima permitida. Então podemos aproximar o coeficiente convectivo médio no último chip como sendo o coeficiente local na posição média, ou seja, em x = 95 mm.
Então, sabendo que o escoamento é laminar, podemos usar a seguinte relação para Nusselt:
Calculando Reynolds para x = 95 mm, temos:
Então, substituindo os valores conhecidos na equação para Nusselt, temos:
Agora, sabendo que o número de Nusselt se relaciona com o coeficiente convectivo através da seguinte equação:
Então, substituindo os valores conhecidos, chegamos em:
E, sabemos que a equação para o calor trocado por convecção é dada por:
Então, substituindo os valores conhecidos nessa equação, chegamos na potência máxima permitida em cada chip:
Passo 3
Agora, vamos analisar o caso onde temos um promotor de turbulência na aresta frontal, ou seja, agora teremos um escoamento turbulento ao longo de todo o comprimento. Faremos a mesma análise feita anteriormente, só que agora iremos utilizar uma correlação de Nusselt para escoamento turbulento, dada por:
Então, substituindo os valores conhecidos, chegamos em:
Agora, sabendo que o número de Nusselt se relaciona com o coeficiente convectivo através da seguinte equação:
Então, substituindo os valores conhecidos, chegamos em:
E, sabemos que a equação para o calor trocado por convecção é dada por:
Então, substituindo os valores conhecidos nessa equação, chegamos na potência máxima permitida em cada chip:
Passo 4
E agora respondendo as duas últimas perguntas do enunciado. Sabemos que é bem melhor orientar a série de chips na direção normal ao escoamento de ar. O motivo disso é porque fazendo isso, teríamos a mesma dissipação de calor em todos os chips, e não uma maior dissipação nos primeiros e menores nos últimos, como é o caso com os chips orientados na direção paralela.