Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 6.Problemas - Ex. 48
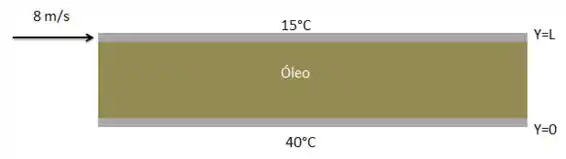
O escoamento de óleo em um mancal pode ser tratado como escoamento paralelo entre duas grandes placas isotérmicas com uma placa que se desloca a uma velocidade constante de 8 m/s e a outra estacionária. Considere o escoamento uniforme com espaçamento de 0,5 mm entre as placas. As temperaturas superior e inferior das placas são 40°C e 15°C, respectivamente. Simplificando e resolvendo as equações da continuidade, da quantidade de movimento e de energia, determine (a) distribuições de velocidade e temperatura do óleo, (b) temperatura máxima e onde ela ocorre e (c) fluxo de calor a partir do óleo para cada placa.
Passo 1
Para o escoamento entre duas placas planas paralelas, a equação da continuidade é dada por:
Assumindo que o escoamento é paralelo às placas, . Então:
Prosseguindo para a equção da quantidade de movimento:
Como vimos anteriormente e ; além disso, como a movimentação do fluido ocorre devido ao movimento da placa, e não devido ao gradiente de pressão, .
Portanto:
Integrando em y:
Integrando novamente:
Vamos agora aplicar as condições de contorno para encontrar as constantes e . Para a velocidade as condições de contorno são:
Em que é o espaçamento entre as placas. Nosso sistema de equações fica:
O perfil de velocidade é:
Agora vamos para a equação de balanço de energia:
Como e só ocorre transferência de calor na direção :
Portanto ficamos com:
Temos condições de calcular :
Substituindo no balanço de energia:
Integrando em :
Integrando em mais uma vez:
Vamos aplicar as condições de contorno para definir as constantes e . Para a temperatura sabemos que:
Então:
Substituindo e no perfil de temperatura:
Passo 2
Com o perfil de temperatura em mãos podemos calcular o ponto de máxima temperatura. Uma breve lembrança dos tempos de cálculo: pontos de máximo ou mínimo de uma função são pontos em que a derivada . Então, o que vamos fazer é derivar em relação a e igualar a zero.
Encontramos a posição em que ocorre a temperatura máxima. Vamos agora aplicar este ponto no perfil de temperatura para encontrar a temperatura máxima do sistema:
Passo 3
Nosso último passo é calcular o fluxo de calor em cada parede. Sabemos que a camada de fluido e contato com a parede tem a mesma velocidade que ela. Como não há diferença de velocidade o fluxo de calor ocorre por condução. Vamos para a primeira parede ():
Já calculamos a derivada de em relação a para descobrir o ponto de máximo. Vamos então substituir a expressão que encontramos:
Na parede a temperatura é de 40°C. Vamos então buscar as propriedades do óleo de motor nesta temperatura:
Substituindo na expressão do fluxo:
Agora vamos repetir o procedimento para a parede :
Na parede o óleo está a 15°C. As propriedades do material nesta temperatura são:
Substituindo as propriedades na equação de condução:
Resposta
Ei, a resposta está no passo a passo :)