Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 05
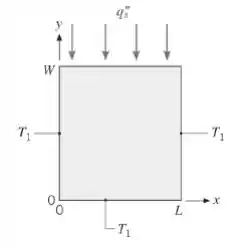
Uma placa retangular bidimensional é submetida a condições de contorno de temperatura especificada em três lados e a condição de fluxo térmico uniforme para dentro da placa em sua superfície superior. Usando a abordagem geral da Seção 4.2, deduza uma expressão para a distribuição de temperaturas na placa.
Passo 1
Fala aí! Olha só, essa questão quer que a gente deduza a expressão da distribuição de temperaturas da placa… Vamos lá!
Tendo nossa condição de superfície superior sendo: , vamos ficar com:
E agora considerando nossas condições de contorno, temos:
Essa solução já temos dada no livro, show né! Então vamos só escrever o resultado que é a equação 4.11 do livro:
Passo 2
Vamos ficar com o seguinte então:
Podemos chamar uma constante de:
Para deixar nossa equação mais organizada, então vamos ter:
Show de bola, estamos quase acabando… Agora vamos então verificar nossas funções:
Sendo assim, vamos ficar com:
Se esse é nosso , então substituindo ele na equação de teremos:
Prontinho! Conseguimos a nossa equação!
Resposta
Ei, a resposta está no passo a passo :)