Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 4.Problemas - Ex. 03

Considere que a placa retangular bidimensional do Problema 4.2 tenha uma condutividade térmica de 50   W / ( m . K ) . Partindo da solução exata para a distribuição de temperaturas, deduza uma expressão para a taxa de transferência de calor, por unidade de espessura, saindo pela superfície inferior ( 0 ≤ x ≤ 2 , y = 0 ) da placa. Calcule a taxa de transferência de calor considerando os cinco primeiros termos não nulos da série infinita.

Passo 1

Fala aí! Olha só, essa questão faz referência a placa da questão anterior, então vamos dar uma olhadinha na imagem dela:

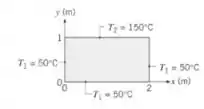
O enunciado quer que a gente calcule a taxa de transferência de calor, considerando os cinco primeiros termos da série… Vamos nessa!

Passo 2

Vamos começar vendo que a taxa de saída de calor é dada por:

q s a í d a ' =   - ∫ x = 0 x = 2 d q y '   ( x ,   0 ) =   - ∫ x = 0 x = 2 - k . ∂ T ∂ y | y = 0   d x = k .   T 2 - T 1 .   ∫ x = 0 x = 2 ∂ θ ∂ y | y = 0   d x

E lembrando que estamos trabalhando com uma série infinita, então:

θ ( x , y ) = T - T 1 T 2 - T 1

θ ( x , y ) = 2 π   .   ∑ n = 1 θ - 1 n + 1 + 1 n . s e n n . π . x L . s e n h n . π . y / L s e n h n . π . W / L

E se juntamos os dois vamos ter que:

q s a í d a ' = k .   T 2 - T 1 .   ∫ x = 0 x = 2 2 π   .   ∑ n = 1 θ - 1 n + 1 + 1 n . s e n n . π . x L . s e n h n . π . y / L s e n h n . π . W / L | y = 0   d x

q s a í d a ' = k .   T 2 - T 1 .   2 π   .   ∑ n = 1 ∞ - 1 n + 1 + 1 n   .   1 s e n h   n . π . x L   .   - c o s   n . π . x L | x = 0 x = 2

q s a í d a ' = k .   T 2 - T 1 .   2 π   .   ∑ n = 1 ∞ - 1 n + 1 + 1 n   .   1 s e n h   n . π / L   .   1 - c o s   n   .   π

Passo 3

Estabelecendo a série infinita de 5 termos não nulos, podemos considerar os cinco primeiros números ímpares positivos, beleza?

Ficamos então com n = 1 ,   3 ,   5 ,   7 ,   9 , e colocando isso na nossa equação ficaremos com:

q s a í d a ' = 50   .   150 - 50 .   2 π   .   { - 1 1 + 1 + 1 1   .   1 s e n h   1 . π / 2   .   1 - c o s 1   .   π   +   - 1 3 + 1 + 1 3   .   1 s e n h   3 . π / 2 . 1 - c o s 3   .   π

- 1 5 + 1 + 1 5 . 1 s e n h   5 . π / 2 . 1 - c o s 5 .   π   +   - 1 7 + 1 + 1 7 . 1 s e n h   7 . π / 2 . 1 - c o s 7 . π   +     - 1 9 + 1 + 1 9 . 1 s e n h   9 . π / 2 . 1 - c o s 9 . π }

q s a í d a ' = 5,611   k W / m

Uhull!! Conseguimos!

Resposta

q s a í d a ' = 5,611   k W / m

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma placa retangular bidimensional está sujeita às condições de contorno especificadas. Usando os resultados da solução exata para a equação do calor apresentados na Seção 4.2, calcule a temperatura n
No método da separação de variáveis (Seção 4.2) para a condução bidimensional em regime estacionário, a constante de separação λ 2 nas Equações 4.6 e 4.7 deve ser uma constante positiva. Mostre que va
Uma placa retangular bidimensional está sujeita às condições de contorno mostradas na figura. Deduza uma expressão para a distribuição de temperaturas em regime estacionário T ( x , y ) .
Uma placa retangular bidimensional é submetida a condições de contorno de temperatura especificada em três lados e a condição de fluxo térmico uniforme para dentro da placa em sua superfície superior.