Seja o Problema 4.5, agora com a placa tendo seção transversal quadrada, .
a) Deduza uma expressão para o fator de forma, , associado à temperatura na superfície superior, tal que , na qual é a temperatura máxima ao longo de .
b) Deduza uma expressão para o fator de forma, , associado à temperatura na superfície superior, , na qual é a temperatura média ao longo de .
c) Determine os fatores de forma que podem ser usados para determinar as temperaturas máxima e média ao longo de . Determine as temperaturas máxima e média para , , e .
Passo 1
Começamos o problema esboçando o esquema bidimensional de condução de calor na placa retangular, obtemos:
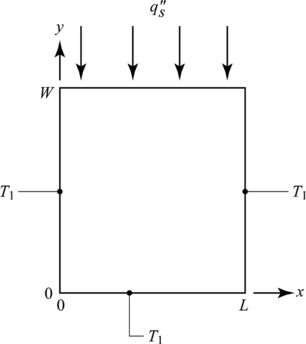
Passo 2
Agora, explicitando as equações bidimensionais de condução de calor em estado estacionário para uma placa retangular:
Aqui, sendo a distribuição de temperatura.
Então, o gradiente de temperatura em relação à direção é e gradiente de temperatura em relação à direção é .
Expressaremos a condição de limite para a placa retangular bidimensional.
Para a superfície limite esquerda:
Para a superfície limite direita:
Sendo o comprimento da placa na direção .
Para a superfície limite inferior:
Para a superfície limite superior:
Sendo:
;
;
.
Desse modo, expressando a forma geral de distribuição de temperatura para uma placa retangular bidimensional nas direções e , temos:
Sendo aqui, a constante térmica associada.
Diferenciando a equação em relação a , obtemos:
Substituindo por :
Passo 3
Substituindo a equação obtida no Passo 2 na equação de fluxo térmico, temos:
Fazendo:
Temos:
Expressando a função em termos de funções ortogonais infinitas:
Sendo aqui, a função ortogonal.
Assim:
Passo 4
Calculando o coeficiente :
Substituindo os termos:
Integrando:
Passo 5
Calculando a constante :
Substituindo :
Passo 6
Calculando a distribuição de temperatura, , para placas retangulares bidimensionais:
Substituindo :
Passo 7
Letra a)
Consideraremos a placa com seção transversal quadrada:
Então, :
E, considerando a temperatura máxima ocorrida no ponto médio da superfície superior, :
A equação da taxa de transferência de calor por condução se dá:
Sendo , então:
Calcule o fator de forma máximo:
Substituindo os termos:
Passo 8
Letra b)
Calculando a distribuiçãode temperatura média, , de placas retangulares bidimensionais:
Substituindo :
Integrando a equação em relação à entre os limites de e :
Substituindo novamente na equação de fator de forma:
Passo 9
Letra c)
Calculando o fator de forma máximo:
Substituindo :
Passo 10
Calculando o fator de forma médio:
Substituindo :
Passo 11
Calculando a temperatura máxima:
Isolando :
Dados:
;
;
;
;
.
Temos:
Passo 12
Calculando a temperatura média:
Isolando :
Dados:
;
Temos: