Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 74
74. Um esquema inovador para o resfriamento de chips de computadores utiliza um termossifão contendo um fluorocarboneto saturado. O chip é soldado no fundo de um recipiente com uma forma parecida com a de uma xícara, no interior do qual o calor é dissipado por ebulição, sendo a seguir transferido para um refrigerante externo (água) pela condensação do vapor sobre a superfície interna de um tubo com parede delgada.
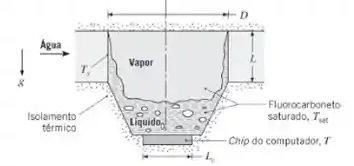
As constantes da ebulição nucleada e as propriedades do fluorocarboneto são as fornecidas no Problema 10.23. Além disso, kl = 0,054 W/(m · K).
(a) Se o chip opera sob condições de regime estacionário e seu fluxo térmico superficial é mantido a 90% do fluxo térmico crítico, qual é sua temperatura T? Qual é a dissipação de potência total, se a dimensão do chip é de Lc = 20 mm em cada lado?
(b) Se o diâmetro do tubo é de D = 30 mm e sua superfície é mantida pela água a Ts = 25°C, qual é o comprimento de tubo L necessário para manter as condições especificadas?
Passo 1
Letra (a)
A relação entre o fluxo de calor na superfície e o fluxo de calor crítico é dada como
O fluxo crítico de calor para a ebulição de um nucleado é expresso como
Substituição dos valores dos parâmetros ,produz o fluxo de calor crítico como
Substituindo na primeira equação teremos:
Ou,
Portanto, a dissipação total de energia do chip é .
O fluxo de calor superficial para a ebulição de nucleados da correlação de Rohsenow é expresso como
Ao substituir os valores dos parâmetros , temos
Substituindo na relação acima, temos
O excesso de temperatura é expresso como
Assim, temos
Portanto, a temperatura do chip de computador é
Passo 2
Letra (b)
A taxa de transferência de calor do chip também pode ser expressa como
Onde, o calor latente corrigido pode ser expresso como
Ao substituir os valores dos parâmetros na relação acima, temos
Da segunda equação para transferência de calor temos:
O número de Reynolds pode ser expresso em termos de vazão mássica de condensado como
Ao substituir os valores dos parâmetros na relação acima, temos o número de Reynolds como
Como o número de Reynolds está entre os intervalos , o fluxo é ondulado laminar.
Da correlação de Kutateladze para a região ondulada laminar, temos
Ao substituir os valores dos parâmetros na equação ácima, temos
Ao substituir , e valores de outros parâmetros na primeira equação para taxa de transferência de calor, temos
Portanto, o comprimento do tubo necessário para manter as condições designadas é