Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 82

A porta frontal de um lava-louças, com largura de 580   m m , tem um respiradouro de ar vertical com 500   m m de altura que apresenta um espaçamento de 20   m m entre a bacia interna, que opera a 52 ° C , e uma placa externa, que é isolada termicamente.

( a ) Determine a perda de calor na superfície da bacia quando o ar ambiente está a 27 ° C .

( b ) Uma mudança no projeto da porta proporciona a oportunidade de aumentar ou diminuir em 10   m m o espaçamento original de 20   m m . Quais recomendações você faria com base em como o espaçamento irá alterar a perda de calor?

Passo 1

Muito bem, entendo a física do problema, note que temos aqui um problema de convecção natural em canais em placas paralelas.

Realizando o esboço do exercício, com os dados do enunciando temos:

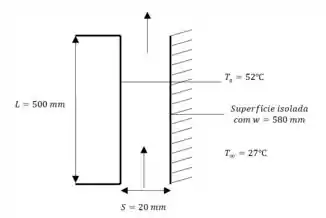
Passo 2

Pra iniciar o exercício, devemos buscar as propriedades do fluido na tabela, porém antes disso devemos determinar a temperatura de filme, pois a convecção natural é analisada nessa temperatura.

Portanto:

T f = T s + T ∞ 2 = 52 + 27 2 = 39,5 + 273 = 312,5   K

Da tabela A-4 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.).

ν = 17,15 × 10 - 6 m 2 s ,   α = 24,4 × 10 - 6 m 2 s ,   k = 27,2 × 10 - 3 W m ∙ K

β = 1 T f = 1 312,5   K = 3,2 × 10 - 3 K

Passo 3

Do enunciando temos que nosso exercício gira em torno de condições isotérmicas, portanto a correlação corresponde é:

N u - s = C 1 R a S S L 2 + C 2 R a S S L 1 2 - 1 2

Onde,

R a S = g β T s - T ∞ S 3 ν α

Para nos ajudar a determinar a perda de calor na superfície da bacia quando o ar ambiente está a 27°C, o que a questão ( a ) pede, iremos precisar da equação abaixo:

N u - s = q A s T s - T ∞ S k

Passo 4

Agora, resolvendo as equações...

R a S = 9,81 m s 2 3 , 2 × 10 - 3 K 52 - 27 K 0,020   m 3 17,15 × 10 - 6 m 2 s 24,4 × 10 - 6 m 2 s = 14988

Logo, da tabela9.3 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.). Para placas isotérmicas e adiabáticas...

C 1 = 144

C 2 = 2,87

Portanto:

N u - s = 144 ( 14988 × 20 500 ) 2 + 2,87 14988 × 20 500 1 2 - 1 2 = 2,92

2,92 = q A s T s - T ∞ S k

q = A s T s - T ∞ k S 2,92

q = 0,500 × 0,580 2 m 2 × 52 - 27 × 0,0272 W m ∙ K 0,020   m × 2,92 = 28,8   W

Passo 5

Para respondermos à questão ( b ) , onde pergunta como o espaçamento irá alterar a perda de calor, caso S = 10   m m ou S = 30   m m .

Basicamente iremos precisar refazer os cálculos para os novos espaçamentos, portanto...

Para S = 10   m m :

R a S = 9,81 m s 2 3 , 2 × 10 - 3 K 52 - 27 K 0,010   m 3 17,15 × 10 - 6 m 2 s 24,4 × 10 - 6 m 2 s = 1874

Logo, da tabela9.3 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.). Para placas isotérmicas e adiabáticas...

C 1 = 144

C 2 = 2,87

Portanto:

N u - s = 144 ( 1874 × 10 500 ) 2 + 2,87 ( 1874 × 10 500 ) 1 2 - 1 2 = 1,32

1,32 = q A s T s - T ∞ S k

q = A s T s - T ∞ k S 2,92

q = 0,500 × 0,580 2 m 2 × 52 - 27 × 0,0272 W m ∙ K 0,010   m × 1,32 = 26,1   W

Passo 6

Para S = 30   m m :

R a S = 9,81 m s 2 3 , 2 × 10 - 3 K 52 - 27 K 0,030   m 3 17,15 × 10 - 6 m 2 s 24,4 × 10 - 6 m 2 s = 50585

Logo, da tabela9.3 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.). Para placas isotérmicas e adiabáticas...

C 1 = 144

C 2 = 2,87

Portanto:

N u - s = 144 ( 50585 × 30 500 ) 2 + 2,87 ( 50585 × 30 500 ) 1 2 - 1 2 = 4,38

4,38 = q A s T s - T ∞ S k

q = A s T s - T ∞ k S 4,38

q = 0,500 × 0,580 2 m 2 × 52 - 27 × 0,0272 W m ∙ K 0,030   m × 4,38 = 28,8   W

Passo 7

Para S = 10   m m :

q = 26,1   W

Para S = 30   m m :

q = 28,8   W

Com o objetivo de minimizar as perdas de calor, recomendaríamos a diminuição do espaçamento...

Resposta

( a ) A perda de calor na superfície da bacia quando o ar ambiente está a 27°C é:

q = 28,8   W

( b )

Para S = 10   m m :

q = 26,1   W

Para S = 30   m m :

q = 28,8   W

Com o objetivo de minimizar as perdas de calor, recomendaríamos a diminuição do espaçamento...

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra vertical de 150m m de diâmetro e 1c m de comprimento tem água escoando em toda sua superfície externa a uma velocidade de 0,5m / s . A temperatura da água é uniforme a 40 ℃ ℃, e a temperatur
Quando nem a convecção natural nem a forçada são desprezíveis, é correto calcular cada uma de forma independente e adicioná-las para determinar a transferência total de calor por convecção?
Considere uma placa vertical de 6m de comprimento a 85 ℃ ℃ no ar a 30 ℃ ℃. Determine a velocidade do movimento forçado acima da qual a transferência de calor por convecção natural é desprezível.
Quando a convecção natural é desprezível e quando não é desprezível na transferência de calor por convecção forçada?
Em que condições a convecção natural aumenta a convecção forçada e em que condições a prejudica?