Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 83
Um aquecedor de ar por convecção natural é constituído por uma série de placas verticais paralelas igualmente espaçadas, que podem ser mantidas a uma temperatura fixa por aquecedores elétricos nelas embutidos. As placas têm comprimento e largura e estão no ar atmosférico quiescente a . A largura total da série não pode ser maior do que .
Para , qual é o espaçamento que maximiza a transferência de calor na série? Para esse espaçamento, quantas placas compõem a série e qual é a taxa de transferência de calor correspondente na série?
Passo 1
Vamos começar identificando a física do problema, a partir do enunciado e da imagem, temos que se trata de um problema de placas verticais paralelas, ou seja, convecção natural em canais.
Com os dados do enunciado e fazendo uma breve representação, temos...
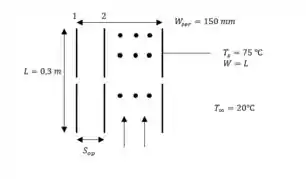
Passo 2
Como todo problema de transferência de calor, devemos determinar os parâmetros do fluido em questão, que é o ar.
Para podemos entrar na tabela, precisamos determinar a temperatura de filme, pois a convecção natural é avaliada nela...
Da tabela A-4 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.).
Passo 3
Para esse exercício, precisamos responder duas perguntas, sendo a primeira dela...
Qual é o espaçamento que maximiza a transferência de calor na série?
Isso significa que devemos determinar o espaçamento ótimo, portanto da tabela 9.3 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.).
Para placas isotérmicas simétricas:
Onde,
Passo 4
Realizando a substituição...
Agora podemos partir pra próxima pergunta:
Para esse espaçamento, quantas placas compõem a série e qual é a taxa de transferência de calor correspondente na série?
Temos que a taxa de calor pode ser determinada por:
Passo 5
Muito bem, como dito antes, nosso problema se trata de convecção natural em canais...
Portanto, temos que para condições isotérmicas:
Onde...
Da tabela 9.3 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.). Para placas isotérmicas simétricas:
Portanto...
Passo 6
Agora, partindo para a determinação do coeficiente convectivo...
Muito bem, agora determinado o número de placas, onde a largura total da série não pode ser maior do que .
Passo 7
Por fim, tendo todos os valores em mãos, basta determinarmos a taxa de transferência de calor:
Resposta
O espaçamento que maximiza a transferência de calor na série é:
Para esse espaçamento, quantas placas compõem a série e qual é a taxa de transferência de calor correspondente na série?