O problema 8.171 descreve uma situação na qual o escoamento em uma longa tubulação, partindo de um tanque elevado, é lentamente reduzido para evitar um aumento grande de pressão (golpe de aríete). Estenda essa análise para predizer e traçar graficamente a programação de fechamento (coeficiente de perda da válvula versus tempo) necessária para manter a pressão máxima na válvula igual ou abaixo de um dado valor durante o processo de interrupção de escoamento do tanque.
Passo 1
Oi pessoal, tudo bem?
Bem, assim como no problema 8.171, para fluxo instável com atrito, modificamos a equação de Bernoulli instável para incluir um termo de perda de carga:
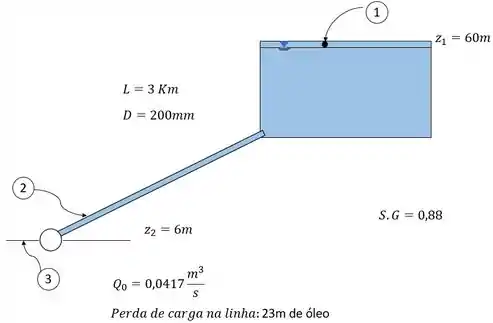
O esboço acima demonstra o esquema de como pode ser analisado a longa tubulação partindo de um tanque elevado.
Consideremos:
;
Então:
Passo 2
Sabe-se que:
E:
Se negligenciarmos a velocidade no tanque, exceto para uma pequena região próxima à extremidade do cano:
Então:
Substituindo valores:
Então:
Onde:
A integral fica da seguinte forma:
Ou:
A pressão cai mais através da válvula:
Para t=0;
Resposta
Fazemos a tabela para cada tempo estimado, com sua respectiva velocidade e :
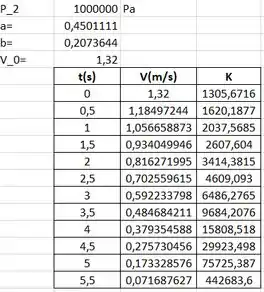
Assim:

