Água a 20°C escoa para cima a 4 m/s por um tubo de 6 cm de diâmetro. O comprimento do tubo entre os pontos 1 e 2 é de 5 m e o ponto 2 está 3 m acima. Um manômetro de mercúrio, conectado entre 1 e 2, mostra uma leitura h = 135 mm, sendo p1 maior. (a) Qual é a variação de pressão (p1 − p2)? (b) Qual é a perda de carga em metros? (c) A leitura do manômetro é proporcional a perda de carga? Explique. (d) Qual é o fator de atrito do escoamento?
Passo 1
E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!
A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 6.3 do livro, chamada “Perda de carga-fator de atrito”.
Nesse problema, temos água a escoando em tubo inclinado de diâmetro . O tubo tem comprimento de , e pontos 2 está acima do ponto 1. Há um manômetro de mercúrio indicando uma leitura .
Pra ilustrar o problema, veja a figura abaixo:
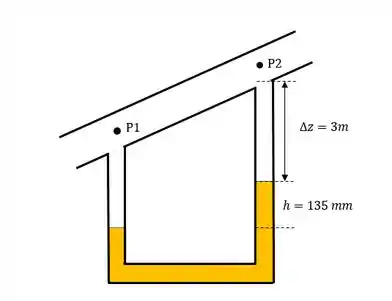
O enunciado nos pede pra calcular a diferença de pressão , a perda de carga, o fator de atrito do escoamento e também nos questiona se A leitura do manômetro é proporcional à perda de carga.
Nos próximos passos, iremos responder todas essas questões. Vem comigo pra gente resolver o problema!

Passo 2
Pra calcular a diferença de pressão, pedida na letra (a) vamos olhar o esquema abaixo, onde adicionamos os pontos A e B:
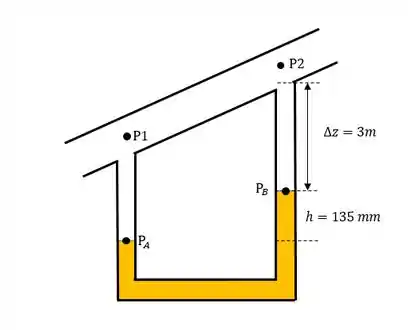
A partir dessa figura, podemos definir, como base na Estática dos Fluidos, três equações:
Sendo: a massa específica da água; e a massa específica do mercúrio.
Combinando essas equações, a gente fica com:
Resolvendo a equação, temos:
Passo 3
Agira, vamos resolver a letra (b).
Pra calcular a perda de carga total no escoamento, devemos usar uma equação originada do balanço de energia mecânica (equação de Bernoulli).
Essa equação relaciona a perda de carga com a queda de pressão e da variação de elevação, da seguinte maneira:
Sendo , o gradiente de pressão entre os pontos 1 e 2; e a variação de elevação entre um ponto a outro do tubo.
Sendo assim:
Passo 4
Agira, iremos resolver a letra (c). Queremos descobrir se a perda de carga total, é proporcional à leitura do manômetro. Pra isso, vamos comprar as equações que usamos nos Passos anteriores:
Vamos reorganizar a primeira equação:
Dividindo tudo por, obtemos:
As devemos lembrar que: :
Ou seja, é sim proporcional a .
Passo 5
Pra finalizar a questão, vamos resolver a letra (d). Para calcular a perda de carga global, usamos a seguinte equação:
Sendo: o fator de atrito que queremos calcular e o comprimento total do tubo.
Basta então que a gente substitua o valor de pra resolver essa parte do problema:
Pronto, matamos a questão!

Resposta
(a) A variação de pressão é
(b) A perda de carga total é
(c) Sim, é sim proporcional a , sendo
(d) O fator de atrito global