Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Frank White - Mecânica dos Fluidos- Ed: 6º - Capítulo 6.Problemas - Ex. 9

Um líquido leve (rho = 950 kg/m3) escoa a uma velocidade média de 10 m/s por um tubo liso de 5 cm de diâmetro. A pressão do fluido é medida em intervalos de 1 m ao longo do tubo, como se segue:

Calcule (a) a perda de carga total, em metros; (b) a tensão de cisalhamento na parede na região totalmente desenvolvida do tubo e (c) o fator de atrito global.

Passo 1

E aí, galera, tudo bem? MecFlu pode parecer difícil, mas cola aqui que eu vou te ajudar!

A primeira ideia que a gente tem que ter da questão é de qual assunto ela faz parte. Esse problema em específico é referente à seção 6.3 do livro, chamada “Perda de carga-fator de atrito”.

Nesse problema, temos um líquido de massa específica ρ = 950   k g / m 3 escoando a uma velocidade v = 10   m / s por um tubo liso de diâmetro D = 0,0 5   m . A pressão é medida em intervalos de 1   m ao longo do tubo, como demonstra a tabela que ilustra a questão.

O enunciado nos pede então para calcularmos a perda de carga total, a tensão de cisalhamento para a região completamente desenvolvida e o fator de atrito global para o escoamento.

Então vem comigo que nos próximos passos a gente vai resolver esse problema!

Passo 2

Em primeiro lugar, vamos resolver a letra (a). Para calcular a perda de carga total no escoamento, devemos usar uma equação originada do balanço de energia mecânica (equação de Bernoulli).

Essa equação relaciona a perda de carga com a queda de pressão e da variação de elevação, da seguinte maneira:

h f = ∆ z + ∆ p ρ g

Sendo ∆ p = 304   k P a - 200   k P a = 104   k P a , o gradiente de pressão total, entre a primeira e a última medida na tabela; e ∆ z = 0 a variação de elevação entre um ponto a outro do tubo, que é horizontal.

Sendo assim:

h f = 104000 P a 950   k g / m 3 9,81   m / s ² = 11,16   m

Passo 3

Agira, iremos resolver a letra (b). Queremos encontrar a tensão de cisalhamento para a queda de pressão na região completamente desenvolvida no escoamento.

Pra gente calcular, vamos usar a equação abaixo:

∆ p ∆ L = 4 τ w D

Sendo: ∆ L a variação de comprimento do tubo para uma determinada queda de pressão e τ w a tensão de cisalhamento que queremos descobrir.

Veja essa imagem que foi retirada do próprio livro, relativa às variações de pressão ao longo de um duto:

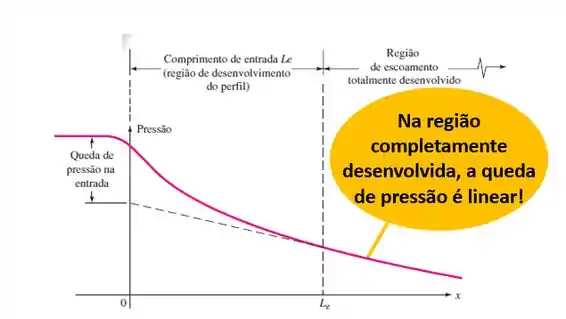
Como é possível ver, na região de escoamento completamente desenvolvido temos uma queda de pressão linear.

Podemos ver, pela tabela que ilustra a questão, que temos uma queda de pressão linear a partir de 4 m de tubo. A queda de pressão por unidade de comprimento dessa região é, olhando novamente a tabela, igual a:

∆ p ∆ L d e s e n v o l d i d o = 13000   P a 1   m =   13000   P a / m

Note que ∆ p ∆ L é como se fosse o coeficiente angular da região linear, e por isso ele constante.

Agora, podemos calcular a tensão de cisalhamento a partir desse ponto:

τ w = D 4 ∆ p ∆ L d e s e n v o l d i d o

τ w = 0,05   m 4   13000   P a / m

τ w = 162,5   P a

Passo 4

Pra finalizar a questão, vamos resolver a letra (c). Para calcular a perda de carga global, usamos a seguinte equação:

h f = f L D v ² 2 g  

Sendo: f o fator de atrito que queremos calcular e L = 6   m o comprimento total do tubo.

Basta então que a gente substitua o valor de h f pra resolver essa parte do problema:

f =   h f D L 2 g v ² = 11,16   m 0,05   m 6   m 2 9,81   m / s ² ( 10   m / s ) ²

f = 0,0182

Pronto, matamos a questão!

Resposta

(a) A perda de carga total é h f = 11,16   m

(b) A tensão de cisalhamento na região totalmente desenvolvida τ w = 162,5   P a

(c) O fator de atrito global f = 0,0182

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Investigue o efeito do diâmetro de tubo sobre a vazão, calculando a vazão gerada por uma diferença de pressão, Δp = 100 kPa, aplicada a um comprimento L = 100 m de um tubo liso. Trace um gráfico da va
Água para resfriamento de perfuratrizes de rocha é bombeada de um reservatório para um canteiro de obras, usando o sistema de tubos mostrado. A vazão deve ser de 38 L s e a água deve deixar o bocal de
Um experimento de atrito de ar consiste de um tubo de latão liso de 63,5 mm de diâmetro interno; a distância entre tomadas de pressão é 1,52 m. A queda de pressão é indicada por um manômetro de tubo e
O aumento de pressão através de uma bomba de água é 75 kPa quando a vazão volumétrica é 25 L s . Se a eficiência da bomba for 80%, determine a potência fornecida para a bomba.
Para o Problema 8.146, que diâmetro seria necessário para o tubo de comprimento 2L gerar a mesma vazão que a do tubo de comprimento L?.