Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 133
Em um processo industrial, produtos de combustão, a uma temperatura e pressão de 2000 K e 1 atm, respectivamente, escoam através de uma longa tubulação com 0,25 m de diâmetro, cuja superfície interna é negra. O gás de combustão contém CO2 e vapor de água, cada um com uma pressão parcial de 0,10 atm. Pode ser considerado que o gás tenha as propriedades
termofísicas do ar atmosférico e que se encontre em escoamento plenamente desenvolvido a uma vazão de . A tubulação é resfriada pela passagem de água em escoamento cruzado sobre sua superfície externa. A velocidade e a temperatura desta água a montante do
sistema são 0,30 m/s e 300 K, respectivamente. Determine a temperatura da parede da tubulação e o fluxo térmico. Sugestão: A emissão da parede da tubulação pode ser desprezada.
Passo 1
É isso ai galerinhaaa !! Vamos continuando?
Bom, a questão nos pediu duas coisas, certo? O fluxo térmico radiante e a temperatura da parede da tubulação !
Bom galerinha, a superfície está absorvendo irradiação emitida pelo gás e calor por convecção da parte interna da tubulação , enquanto perde calor por convecção na parte externa , certo?
Se nós fizermos um balanço de energia:
A irradiação pode ser reescrita como:
Enquanto a convecção:
Então:
Shoooow !!
Agora vamos ver o que já temos?
Então nós só precisamos achar , e !!
Passo 2
Para achar a emissividade do vamos dar uma olhada nesta figura aqui:
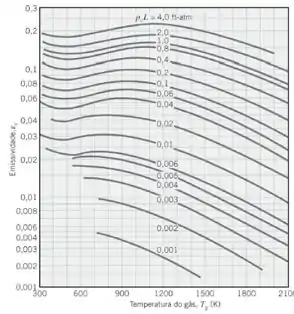
E para o vapor de água esta:
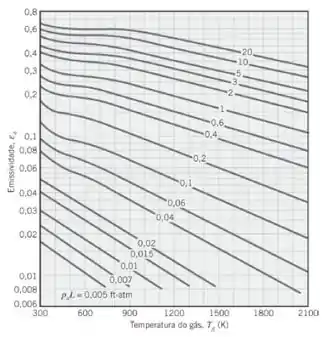
Para cilindros:
Mas o gráfico nos pediu em transformando:
Interceptando no gráfico, quando
Mas o que nós queremos aqui é !!
E para isso nós vamos usar uma formulinha:
Para achar nós vamos precisar de mais um gráfico:
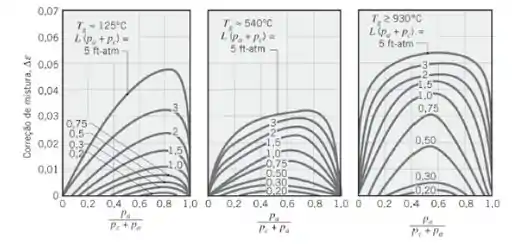
Calculando o que ainda não temos:
No último gráfico:
Ufaaaa !! Agora sim:
Passo 3
Agora nós precisamos calcular o coeficiente, mas para isso precisamos de Reynolds:
Para o fluxo interno, podemos obter as propriedades do fluido na Tabela A – 4 a 2000 K:
Como:
Então:
Como o fluxo é turbulento nós podemos usar a correlação de Dittus – Boelter:
Substituindo:
Passo 4
Para calcular o coeficiente externo também precisamos de Reynolds, mas aqui é um pouco diferente:
Para calcular o coeficiente externo nós podemos obter as propriedades para a água na Tabela A – 6 a 300 K:
Lembrando que:
Então:
Aqui nós podemos usar a correlação de Zukauskas:
Assumindo que e substituindo:
Passo 5
Substituindo tudo que achamos no balanço:
Resolvendo:
Com a temperatura nós podemos achar o fluxo térmico de calor trocado!!
Agora basta nós substituir a temperatura da superfície em um lado da igualdade que vimos no Passo 1:
E é isso aí galerinha !! Mais uma vencida com sucesso !!