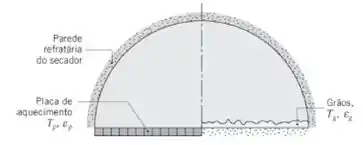
Um secador de grãos é constituído por um longo duto semicircular com raio R = 1 m. Metade da superfície da base é ocupada por uma placa eletricamente aquecida, com emissividade εp = 0,8, enquanto a outra metade suporta os grãos a serem secos, que têm uma emissividade de εg = 0,9. Em um processo de secagem em batelada, no qual a temperatura dos grãos é de Tg = 330 K, 2,50 kg de água devem ser removidos por metro de comprimento do duto em um período de 1 hora.

1. Desprezando a transferência de calor por convecção, determine a temperatura Tp que a placa aquecedora deve ter.
2. Se o vapor de água é removido do duto pelo escoamento de ar seco, qual é o valor do coeficiente de transferência de massa hm que deve ser mantido pelo escoamento?
3. Se o ar estiver a 300 K, a hipótese de convecção desprezível se justifica?

A letra (b) nos pediu para achar o do coeficiente de transferência de massa hm que deve ser mantido pelo escoamento se o vapor de água é removido do duto pelo escoamento de ar seco, tranquilo?

A taxa de evaporação é dada por:

Isolando o que queremos:

Sabendo que:

Então:

Olhando na Tabela A – 6, para o vapor de água a 330 K:

Substituindo:

E assim nós chegamos a mais uma respostaa !!

Na letra (c), queremos saber se o ar estiver a 300 K, a hipótese de convecção desprezível se justifica?

Bom, se a convecção for desprezível , certo?

Nós sabemos que:

E o calor convectivo é dado por:

Nós não temos o coeficiente convectivo, mas podemos calcular:

Lembrando que:

Então:

Olhando na Tabela A – 4 para o ar próximo a 300 K:

Na Tabela A – 8, para o vapor de água e ar:

Substituindo:

No calor convectivo:

Como nós podemos desconsiderar a convecção !!

Ufaaa !! Acabamos !!